题目内容
有以下四个命题:
①如果
•
=
•
且
≠0,那么
=
;
②如果
•
=0,那么
=
或
=
;
③△ABC中,如果
•
>0,那么△ABC是钝角三角形;
④△ABC中,如果
•
=0,那么△ABC为直角三角形.
其中正确命题的个数是( )
①如果
| a |
| b |
| b |
| c |
| b |
| a |
| c |
②如果
| a |
| b |
| a |
| 0 |
| b |
| 0 |
③△ABC中,如果
| AB |
| BC |
④△ABC中,如果
| AB |
| BC |
其中正确命题的个数是( )
分析:利用非零向量
•
=0?
⊥
及数量积的定义即可判断出答案.
| a |
| b |
| a |
| b |
解答:解:①∵
•
=
•
且
≠
,∴
•(
-
)=0,
与
不一定相等,故①不正确;
②∵
•
=0,∴
=
,或
=
,或
⊥
,故不正确;
③在△ABC中,∵
•
>0,∴
•
<0,∴∠ABC是钝角,故△BAC是钝角三角形,因此正确;
④在△ABC中,∵
•
=0,∴
⊥
,即AB⊥BC,∴∠ABC=90°,∴△ABC是直角三角形,故正确.
综上可知:只有③④正确,即正确命题的个数是2.
故选C.
| a |
| b |
| b |
| c |
| b |
| 0 |
| b |
| a |
| c |
| a |
| c |
②∵
| a |
| b |
| a |
| 0 |
| b |
| 0 |
| a |
| b |
③在△ABC中,∵
| AB |
| BC |
| BA |
| BC |
④在△ABC中,∵
| AB |
| BC |
| AB |
| BC |
综上可知:只有③④正确,即正确命题的个数是2.
故选C.
点评:熟练掌握向量的数量积及非零向量
•
=0?
⊥
是解题的关键.
| a |
| b |
| a |
| b |

练习册系列答案
相关题目
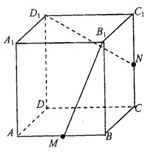 16、如图所示,在正方体ABCD-A1B1C1D1中,M、N分别是棱AB、CC1的中点,△MB1P的顶点P在棱CC1与棱C1D1上运动,有以下四个命题:
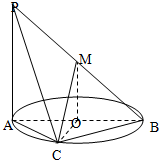
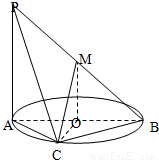
16、如图所示,在正方体ABCD-A1B1C1D1中,M、N分别是棱AB、CC1的中点,△MB1P的顶点P在棱CC1与棱C1D1上运动,有以下四个命题: 如图AB为圆O的直径,点C在圆周上(异于A,B点)直线PA垂直于圆所在的平面,点M为线段PB的中点,有以下四个命题:
如图AB为圆O的直径,点C在圆周上(异于A,B点)直线PA垂直于圆所在的平面,点M为线段PB的中点,有以下四个命题: 如图AB为圆O的直径,点C在圆周上(异于A,B点)直线PA垂直于圆所在的平面,点M为线段PB的中点,有以下四个命题:其中正确的命题是
如图AB为圆O的直径,点C在圆周上(异于A,B点)直线PA垂直于圆所在的平面,点M为线段PB的中点,有以下四个命题:其中正确的命题是