题目内容
已知首项为a(a≠0)的数列{an}的前n项和为Sn,,若对任意的正整数m、n,都有
=(
)2.
(Ⅰ)证明:数列{an}是等差数列;
(Ⅱ)若a=1,数列{bn}的首项为b(b≠1),第n(n∈N*,n≥2)项bn是数列{an}的第bn-1项,求证:数列|bn-1|为等比数列;
(Ⅲ)若对(Ⅱ)中的数列{an}和{bn}及任意正整数n,均有2an+bn+11≥0成立,求实数b的最小值.
| Sn |
| Sm |
| n |
| m |
(Ⅰ)证明:数列{an}是等差数列;
(Ⅱ)若a=1,数列{bn}的首项为b(b≠1),第n(n∈N*,n≥2)项bn是数列{an}的第bn-1项,求证:数列|bn-1|为等比数列;
(Ⅲ)若对(Ⅱ)中的数列{an}和{bn}及任意正整数n,均有2an+bn+11≥0成立,求实数b的最小值.
(Ⅰ)证明:在
=(
)2中,取m=1,得
=n2,即Sn=n2a,
当n≥2时,Sn-1=(n-1)2a,
∴an=Sn-Sn-1=n2a-(n-1)2a=(2n-1)a,
当n=1时,a1=a也适合上式,
∴an=(2n-1)a,n∈N+,
∵an+1-an=2a,
∴{an}是以a为首项,2a为公差的等差数列.
(Ⅱ)证明:当a=1时,由(Ⅰ)可得an=2n-1,
∴bn=2bn-1-1,
即有bn-1=2(bn-1-1),
b1-1=b-1≠0,
∴{bn-1}是以b-1为首项,2为公比的等比数列.
(Ⅲ)由(Ⅱ)知,bn-1=(b-1)•2n-1,
∴bn=1+(b-1)•2n-1,
∴由题意得,不等式22n-1+(b-1)•2n-1+12≥0对任意正整数n恒成立,
即b-1≥-
=-(2n+
)恒成立.
设t=2n(t=2,4,8,…),则b-1>-(t+
)恒成立,
对于函数y=x+
,
y′= 1-
=
.
当x∈(-2
,2
)时,y′<0,当x∈(-∞,-2
)和(2
,+∞)时,y′>0,
∴函数y=x+
在(-2
,2
)上单调减,在(-∞,-2
)和(2
,+∞)上单调增.
又当x=4时,y=10;当x=8时,y=11,∴y=t+
的最小值是10.∴b-1≥[-(2n+
)]min=-10.
即b≥-9,
∴实数b的最小值是-9.
| Sn |
| Sm |
| n |
| m |
| Sn |
| 1 |
当n≥2时,Sn-1=(n-1)2a,
∴an=Sn-Sn-1=n2a-(n-1)2a=(2n-1)a,
当n=1时,a1=a也适合上式,
∴an=(2n-1)a,n∈N+,
∵an+1-an=2a,
∴{an}是以a为首项,2a为公差的等差数列.
(Ⅱ)证明:当a=1时,由(Ⅰ)可得an=2n-1,
∴bn=2bn-1-1,
即有bn-1=2(bn-1-1),
b1-1=b-1≠0,
∴{bn-1}是以b-1为首项,2为公比的等比数列.
(Ⅲ)由(Ⅱ)知,bn-1=(b-1)•2n-1,
∴bn=1+(b-1)•2n-1,
∴由题意得,不等式22n-1+(b-1)•2n-1+12≥0对任意正整数n恒成立,
即b-1≥-
| 22n-1+12 |
| 2n-1 |
| 24 |
| 2n |
设t=2n(t=2,4,8,…),则b-1>-(t+
| 24 |
| t |
对于函数y=x+
| 24 |
| x |
y′= 1-
| 24 |
| x2 |
(x+2
| ||||
| x2 |
当x∈(-2
| 6 |
| 6 |
| 6 |
| 6 |
∴函数y=x+
| 24 |
| x |
| 6 |
| 6 |
| 6 |
| 6 |
又当x=4时,y=10;当x=8时,y=11,∴y=t+
| 24 |
| t |
| 24 |
| 2n |
即b≥-9,
∴实数b的最小值是-9.

练习册系列答案
 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
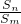 =
=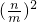 .
.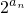 +bn+11≥0成立,求实数b的最小值.
+bn+11≥0成立,求实数b的最小值.