题目内容
某人为了观看2010年南非足球世界杯,从2006年起,每年的5月1日到银行存入a元的定期储蓄,若年利率为p且保持不变,并约定每年到期,存款的本息均自动转为新的一年的定期,到2010年的5月1日将所有存款及利息全部取出,则可取出钱(元)的总数为( )
| A、a(1+p)4 | ||
| B、a(1+p)5 | ||
C、
| ||
D、
|
分析:存入a元,一年后存款及利息是a(1+p),二年后存款及利息是a(1+p)2,…依此类推,四年后存款及利息是a(1+p)4,由此知,到2010年的5月1日将所有存款及利息总数是a(1+p)4+a(1+p)3+a(1+p)2+a(1+p)是一个等比数列的和,用等比数列求和公式求解.
解答:解:依题意,可取出钱的总数为
a(1+p)4+a(1+p)3+a(1+p)2+a(1+p)
=a•
=
[(1+p)5-(1+p)].
故选D.
a(1+p)4+a(1+p)3+a(1+p)2+a(1+p)
=a•
| (1+p)[1-(1+p)4] |
| 1-(1+p) |
| a |
| p |
故选D.
点评:本题是等比数列在实际生活中的应用题,与每个人的生活密切相关,具有强烈的生活气息,高考中非常重视应用题的考查,同学们在平时练习中要多加注意此类题型.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
某人为了观看2010年南非世界杯,2004年起,每年5月10日到银行存入m元定期储蓄,若年利率为r且保持不变,并约定每年到期存款均自动转为新的一年定期,到2010年5月10日将所有存款和利息全部取回,则可取回钱的总数(元)为( )
| A、m(1+r)6 | ||
| B、m(1+r)7 | ||
C、
| ||
D、
|
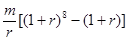 D.
D.
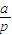 [(1+p)4-(1+p)]
[(1+p)4-(1+p)]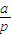 [(1+p)5-(1+p)]
[(1+p)5-(1+p)]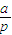 [(1+p)4-(1+p)]
[(1+p)4-(1+p)]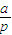 [(1+p)5-(1+p)]
[(1+p)5-(1+p)]