题目内容
某公司仓库A存有货物12吨,仓库B存有货物8吨,现按7吨、8吨和5吨把货物分别调运给甲、乙、丙,从仓库A运货物给甲、乙、丙每吨货物的运费分别为8元、6元、9元;从仓库B运货物到商店甲、乙、丙,每吨货物的运费分别为3元、4元、5元.问应如何安排调运方案,才能得到从两个仓库货物到三个商店的总运费最少?分析:由于题目中量比较多,所以最好通过列出表格以便清晰地展现题目中的条件.设出仓库A运给甲、乙商店的货物吨数可得运到丙商店的货物吨数,列出可行域,目标函数,利用相关的知识求解.
解答:解:将已知数据列成下表:
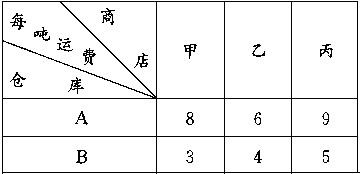
设仓库A运给甲、乙商店的货物分别为x吨,y吨,则仓库A运给丙商店的货物为(12-x-y)吨,
从而仓库B运给甲、乙、丙商店的货物分别为(7-x)吨、(8-y)吨、[5-(12-x-y)]=(x+y-7)吨,
于是总运费为:Z=8x+6y+9(12-x-y)+3(7-x)+4(8-y)+5(x+y-7)=x-2y+126.
∴线性约束条件为
,即
.
目标函数为:z=x-2y+126.作出上述不等式组表示的平面区域,即可行域,如图中阴影部分所示: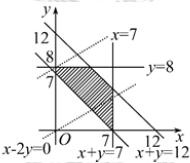
作出直线l:x-2y=0,把直线l平行移动,显然当直线l移动到过点(0,8),
在可行域内,z=x-2y+126.
取得最小值zmin=0-2×8+126=110,即x=0,y=8时总运费最少.
安排的调运方案如下:
仓库A运给甲、乙、丙商店的货物分别为0吨、8吨、4吨,
仓库B运给甲、乙、丙商店的货物分别为7吨、0吨、1吨,此时可使得从两个仓库运货物到三个商店的总运费最少.

设仓库A运给甲、乙商店的货物分别为x吨,y吨,则仓库A运给丙商店的货物为(12-x-y)吨,
从而仓库B运给甲、乙、丙商店的货物分别为(7-x)吨、(8-y)吨、[5-(12-x-y)]=(x+y-7)吨,
于是总运费为:Z=8x+6y+9(12-x-y)+3(7-x)+4(8-y)+5(x+y-7)=x-2y+126.
∴线性约束条件为
|
|
目标函数为:z=x-2y+126.作出上述不等式组表示的平面区域,即可行域,如图中阴影部分所示:

作出直线l:x-2y=0,把直线l平行移动,显然当直线l移动到过点(0,8),
在可行域内,z=x-2y+126.
取得最小值zmin=0-2×8+126=110,即x=0,y=8时总运费最少.
安排的调运方案如下:
仓库A运给甲、乙、丙商店的货物分别为0吨、8吨、4吨,
仓库B运给甲、乙、丙商店的货物分别为7吨、0吨、1吨,此时可使得从两个仓库运货物到三个商店的总运费最少.
点评:考查简单线性规划的知识,在做此类题时,一般数据较多,所以列出表格,整理数据.

练习册系列答案
 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案
相关题目