题目内容
袋子A和B中装有若干个均匀的红球和白球,从A中摸出一个红球的概率是
,从B中摸出一个红球的概率是
.现从两个袋子中有放回的摸球•
(I)从A中摸球,每次摸出一个,共摸5次.求:
(i)恰好有3次摸到红球的概率;
(ii)设摸得红球的次数为随机变量X,求X的期望;
(Ⅱ)从A中摸出一个球,若是白球则继续在袋子A中摸球,若是红球则在袋子B中摸球,若从袋子B中摸出的是白球则继续在袋子B中摸球,若是红球则在袋子A中摸球,如此反复摸球3次,计摸出的红球的次数为Y,求Y的分布列以及随机变量Y的期望.
| 1 |
| 3 |
| 2 |
| 3 |
(I)从A中摸球,每次摸出一个,共摸5次.求:
(i)恰好有3次摸到红球的概率;
(ii)设摸得红球的次数为随机变量X,求X的期望;
(Ⅱ)从A中摸出一个球,若是白球则继续在袋子A中摸球,若是红球则在袋子B中摸球,若从袋子B中摸出的是白球则继续在袋子B中摸球,若是红球则在袋子A中摸球,如此反复摸球3次,计摸出的红球的次数为Y,求Y的分布列以及随机变量Y的期望.
分析:(I)(i)由题意知本题是在相同的条件下进行的试验,且事件发生的概率相同,可以看作独立重复试验,根据独立重复试验公式得到结果.
(ii)由题意知从A中有放回地摸球,每次摸出一个,是独立重复试验,根据独立重复试验公式得到答案.
(II)由题意知计摸出的红球的次数为Y,随机变量Y的取值为0,1,2,3;由独立试验概率公式得到概率,写出分布列和期望.
(ii)由题意知从A中有放回地摸球,每次摸出一个,是独立重复试验,根据独立重复试验公式得到答案.
(II)由题意知计摸出的红球的次数为Y,随机变量Y的取值为0,1,2,3;由独立试验概率公式得到概率,写出分布列和期望.
解答:解:(Ⅰ)(i)由题意知本题是在相同的条件下进行的试验,且事件发生的概率相同,可以看作独立重复试验,
根据独立重复试验公式得到,恰好有3次摸到红球的概率:C53×(
)3×(
)2=
.
(ii)由题意知从A中有放回地摸球,每次摸出一个,是独立重复试验,
根据独立重复试验公式得到:X~B(5,
),
∴EX=5×
=
.
(II)∵随机变量Y的取值为0,1,2,3;且:
P(Y=0)=(1-
)3=
;
P(Y=1)=
×(
)2+(1-
)×
×
+
×(1-
)2=
;
P(Y=2)=
×(1-
)2+(1-
)×
×
+
×(1-
)2=
;
P(Y=3)=(1-
)×
×
=
;
随机变量Y的分布列是:
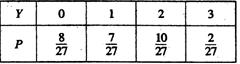
∴Y的数学期望是EY=
.
根据独立重复试验公式得到,恰好有3次摸到红球的概率:C53×(
| 1 |
| 3 |
| 2 |
| 3 |
| 40 |
| 243 |
(ii)由题意知从A中有放回地摸球,每次摸出一个,是独立重复试验,
根据独立重复试验公式得到:X~B(5,
| 1 |
| 3 |
∴EX=5×
| 1 |
| 3 |
| 5 |
| 3 |
(II)∵随机变量Y的取值为0,1,2,3;且:
P(Y=0)=(1-
| 1 |
| 3 |
| 8 |
| 27 |
P(Y=1)=
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| 7 |
| 27 |
P(Y=2)=
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| 10 |
| 27 |
P(Y=3)=(1-
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| 2 |
| 27 |
随机变量Y的分布列是:

∴Y的数学期望是EY=
| 11 |
| 9 |
点评:解决离散型随机变量分布列问题时,主要依据概率的有关概念和运算,同时还要注意题目中离散型随机变量服从什么分布,若服从特殊的分布则运算要简单的多.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目