Question

（本小题16分）

已知定义在上的函数和数列满足下列条件：，，当时，，且存在非零常数使恒成立．

（1）若数列是等差数列，求的值；

（2）求证：数列为等比数列的充要条件是．

（3）已知，，且（），数列的前项是，对于给定常数，若的值是一个与无关的量，求的值．

Answer 1

解:（1）由已知，，得

 

由数列是等差数列，得

所以，，，得．       ………4分

（2）充分性证明：若，则由已知，

得，

所以，是等比数列．                               ………6分

必要性证明：若是等比数列，设公比为，则有，

由及得

又，

所以数列是以为首项，公比为的等比数列，

所以，

当时，   ………8分

①若，，（）

对也成立．

数列是公差为的等差数列，不可能是等比数列，所以，

②，，（）

对也成立．

所以，

由数列是等比数列知，，即，

即对任意非零实数都成立．

综上可得：数列为等比数列的充要条件是．………10分

（3）由（Ⅱ）知，数列是首项为，公比为的等比数列，即，

是一个常数，

故数列是等差数列，设公差为，

依题意，

，

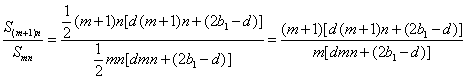当且仅当或时，是一个与无关的常数，

不成立，

所以，即，

．                                                   ………16分