题目内容
在平面几何里，有勾股定理：“设△ABC的两边AB，AC互相垂直，则|AB|2+|AC|2=|BC|2”拓展到空间，类比平面几何的勾股定理，“设三棱锥A-BCD的三个侧面ABC、ACD、ADB 两两相互垂直，则可得”（ ）A．|AB|2+|AC|2+|AD|2=|BC|2+|CD|2+|BD|2
B．S2△ABC×S2△ACD×S2△ADB=S2△BCD
C．S△ABC2+S△ACD2+S△ADB2=S△BCD2
D．|AB|2×|AC|2×|AD|2=|BC|2×|CD|2×|BD|2
【答案】分析：斜边的平方等于两个直角边的平方和，可类比到空间就是斜面面积的平方等于三个直角面的面积的平方和，边对应着面．
解答：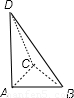
解：由边对应着面，
边长对应着面积，
由类比可得：
SBCD2=SABC2+SACD2+SADB2．
故选C．
点评：本题考查了从平面类比到空间，属于基本类比推理．
解答：
解：由边对应着面，边长对应着面积，
由类比可得：
SBCD2=SABC2+SACD2+SADB2．
故选C．
点评：本题考查了从平面类比到空间，属于基本类比推理．
练习册系列答案
新思维假期作业暑假吉林大学出版社系列答案
蓝天教育暑假优化学习系列答案
相关题目
的两边AB、AC互相垂直，则
。”拓展到空间，类比平面几何的勾股定理，研究三棱锥的侧面积与底面积间的关系，可以得到的正确结论是：“设三棱锥A-BCD的三个侧面ABC、ACD、ADB两两互相垂直，则 ”
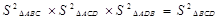
D．AB2×AC2×AD2=BC2
×CD2 ×BD2