题目内容
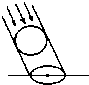 如图,一个广告气球被一束入射角为45°的平行光线照射,其投影是一个最长的弦长为5米的椭圆,则这个广告气球直径是
如图,一个广告气球被一束入射角为45°的平行光线照射,其投影是一个最长的弦长为5米的椭圆,则这个广告气球直径是分析:根据光线,广告气球的半径和椭圆的最长的弦之间的位置关系,得到这三者构成一个等腰直角三角形,要求的球的直径是等腰直角三角形的直角边,在直角三角形中,利用三角函数解出结果.
解答:解:由题意知光线,广告气球的半径和椭圆的最长的弦,
三者构成一个等腰直角三角形,
要求的球的直径是等腰直角三角形的直角边,
∴广告气球的直径是5cos45°=
故答案为:
三者构成一个等腰直角三角形,
要求的球的直径是等腰直角三角形的直角边,
∴广告气球的直径是5cos45°=
5
| ||
| 2 |
故答案为:
5
| ||
| 2 |
点评:本题考查平行投影及平行投影作图法,考查直角三角形的边长之间的关系,是一个基础题,这种题目运算量不大,又是同学们感兴趣的问题,题意比较新颖.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
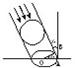 11、如图,一个广告气球被一束入射角为α的平行光线照射,其投影是一个长半轴为5 m的椭圆,则制作这个广告气球至少需要的面料是
11、如图,一个广告气球被一束入射角为α的平行光线照射,其投影是一个长半轴为5 m的椭圆,则制作这个广告气球至少需要的面料是
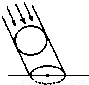 如图,一个广告气球被一束入射角为45°的平行光线照射,其投影是一个最长的弦长为5米的椭圆,则这个广告气球直径是 米.
如图,一个广告气球被一束入射角为45°的平行光线照射,其投影是一个最长的弦长为5米的椭圆,则这个广告气球直径是 米.