题目内容
f(x)=(1+2x)m+(1+3x)n(m,n∈N*)的展开式中x的系数为13,则x2的系数为
- A.31
- B.40
- C.31或40
- D.71或80
C
分析:利用二项展开式的通向公式得x的系数,列出方程求得n,m,然后利用二项展开式的通项公式求出x2的系数即可.
解答:(1+2x)m的展开式中x的系数为2Cm1=2m,
(1+3x)n的展开式中x的系数为3Cn1=3n
∴3n+2m=13
∴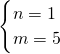 或
或
(1+2x)m的展开式中的x2系数为22Cm2,
(1+3x)n的展开式中的x2系数为32Cn2
∴当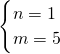 时,x2的系数为22Cm2+32Cn2=40
时,x2的系数为22Cm2+32Cn2=40
当 时,x2的系数为22Cm2+32Cn2=31
时,x2的系数为22Cm2+32Cn2=31
故选C.
点评:本题主要考查了二项展开式的通项公式,通项公式是解决二项展开式的特定项问题的工具,属于中档题.
分析:利用二项展开式的通向公式得x的系数,列出方程求得n,m,然后利用二项展开式的通项公式求出x2的系数即可.
解答:(1+2x)m的展开式中x的系数为2Cm1=2m,
(1+3x)n的展开式中x的系数为3Cn1=3n
∴3n+2m=13
∴
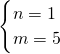 或
或
(1+2x)m的展开式中的x2系数为22Cm2,
(1+3x)n的展开式中的x2系数为32Cn2
∴当
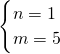 时,x2的系数为22Cm2+32Cn2=40
时,x2的系数为22Cm2+32Cn2=40当
 时,x2的系数为22Cm2+32Cn2=31
时,x2的系数为22Cm2+32Cn2=31故选C.
点评:本题主要考查了二项展开式的通项公式,通项公式是解决二项展开式的特定项问题的工具,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目