题目内容
泉州市组织群众性登清源山健身活动,招募了 名师生志愿者,现将所有志愿者按年龄情况分为
名师生志愿者,现将所有志愿者按年龄情况分为 等六组,其频率分布直方图如下图所示: 已知
等六组,其频率分布直方图如下图所示: 已知 之间的志愿者共
之间的志愿者共 人.
人.
(1)求 和
和 之间的志愿者人数
之间的志愿者人数 ;
;
(2)已知 和
和 之间各有
之间各有 名数学教师,现从这两个组中各选取
名数学教师,现从这两个组中各选取 人担任接待工作,设两组的选择互不影响,求两组选出的人中都至少有
人担任接待工作,设两组的选择互不影响,求两组选出的人中都至少有 名数学教师的概率?
名数学教师的概率?
(3)组织者从 之间的志愿者(其中共有
之间的志愿者(其中共有 名女教师,其余全为男教师)中随机选取
名女教师,其余全为男教师)中随机选取 名担任后勤保障工作,其中女教师的人数为
名担任后勤保障工作,其中女教师的人数为 ,求
,求 的分布列和数学期望
的分布列和数学期望 .
.

【答案】
(1)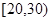 之间的志愿者人数24
(2)
之间的志愿者人数24
(2)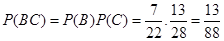
(3)分布列为
|
|
|
|
|
|
|
|
|
|
数学期望为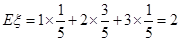
【解析】本试题主要是考查了直方图的运用,以及分布列的求解和数学期望公式的 运用。
(1)根据直方图中面积代表频率先分析各个组的频率值,然后得到样本容量的值和给定区间的频数。
(2)根据题意可知已知【20,25)和【30,35)之间各有2名数学教师,现从这两个组中各选取2人担任接待工作,设两组的选择互不影响,求两组选出的人中都至少有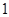 名数学教师的概率值,可以运用古典概型概率公式得到。
名数学教师的概率值,可以运用古典概型概率公式得到。
(3)利用随机变量的取值以及各个取值的概率值得到分布列和数学期望值的运算
解: (1)设频率分布直方图中 个组的频率分别为
个组的频率分别为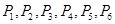
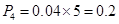 ,所以,
,所以, 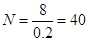 ……………2分
……………2分
由题意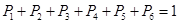
而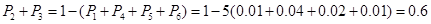
所以, 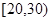 之间的志愿者人数
之间的志愿者人数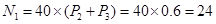 …………2分
…………2分
(2)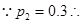
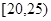 之间有
之间有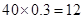 人……………5分
人……………5分
设从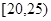 之间取
之间取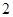 人担任接待工作,其中至少有1名数学教师的事件为
人担任接待工作,其中至少有1名数学教师的事件为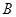 ;
;
从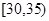 之间取
之间取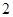 人担任接待工作,其中至少有1名数学教师的事件为
人担任接待工作,其中至少有1名数学教师的事件为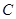
因为两组的选择互不影响,为相互独立事件
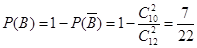 ,
,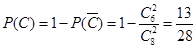 ……………2分
……………2分
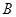 与
与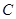 为相互独立事件,同时发生可记做
为相互独立事件,同时发生可记做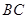
所以, ……………2分
……………2分
(3) 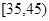 之间共有
之间共有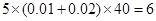 人,其中
人,其中 名女教师,
名女教师,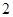 名男教师
名男教师
从中选取三人,则女教师的数量为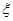 的取值可为
的取值可为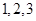
所以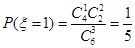 ;
;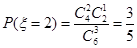 ;
;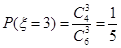 ………3分
………3分
所以,分布列为
|
|
|
|
|
|
|
|
|
|
所以,数学期望为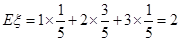

练习册系列答案
相关题目
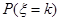
 某区组织群众性登山健身活动,招募了N名师生志愿者,将所有志愿者现按年龄情况分为15~20,20~25,25~30,30~35,35~40,40~45等六个层次,其频率分布直方图如图所示:已知30~35之间的志愿者共8人.
某区组织群众性登山健身活动,招募了N名师生志愿者,将所有志愿者现按年龄情况分为15~20,20~25,25~30,30~35,35~40,40~45等六个层次,其频率分布直方图如图所示:已知30~35之间的志愿者共8人.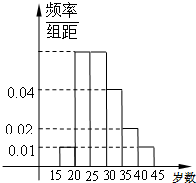 某单位组织群众性登山健身活动,招募了N名师生志愿者,将所有志愿者现按年龄情况分为15-20,20-25,25-30,30-35,35-40,40-45等六个层次,其频率分布直方图如图所示:已知30-35之间的志愿者共8人.
某单位组织群众性登山健身活动,招募了N名师生志愿者,将所有志愿者现按年龄情况分为15-20,20-25,25-30,30-35,35-40,40-45等六个层次,其频率分布直方图如图所示:已知30-35之间的志愿者共8人. 名师生志愿者,将所有志愿者现按年龄情况分为
名师生志愿者,将所有志愿者现按年龄情况分为 等六个层次,其频率分布直方图如图所示: 已知
等六个层次,其频率分布直方图如图所示: 已知 之间的志愿者共
之间的志愿者共 人.
人. 之间的志愿者人数
之间的志愿者人数 ;
; 和
和 名英语教师,现从这两个层次各选取
名英语教师,现从这两个层次各选取 之间的志愿者(其中共有
之间的志愿者(其中共有 名女教师,其余全为男教师)中随机选取
名女教师,其余全为男教师)中随机选取 名担任后勤保障工作,其中女教师的数量为
名担任后勤保障工作,其中女教师的数量为 ,求
,求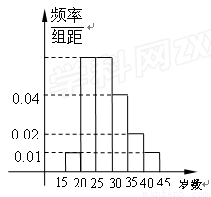
 某单位组织群众性登山健身活动,招募了N名师生志愿者,将所有志愿者现按年龄情况分为15-20,20-25,25-30,30-35,35-40,40-45等六个层次,其频率分布直方图如图所示:已知30-35之间的志愿者共8人.
某单位组织群众性登山健身活动,招募了N名师生志愿者,将所有志愿者现按年龄情况分为15-20,20-25,25-30,30-35,35-40,40-45等六个层次,其频率分布直方图如图所示:已知30-35之间的志愿者共8人.