题目内容
在△ABC中，已知面积S△ABC=6
，a=3，b=8，求角C及边c 的值．
| 3 |
分析：根据△ABC的面积求出sinC的值，可得角C的值，应用余弦定理求出边c 的值．
解答：解：由题意可得 6
=
×3×8 sinC，∴sinC=
，∴C=60° 或120°．
当 C=60°时，根据余弦定理可得 c2=32+82-2×3×8cos60°=61，∴c=
．
当C=120°时，根据余弦定理可得 c2=32+82-2×3×8cos120°=85，∴c=
．
综上，C=60° 或120°，c=
或
．
| 3 |
| 1 |
| 2 |
| ||
| 2 |
当 C=60°时，根据余弦定理可得 c2=32+82-2×3×8cos60°=61，∴c=
| 61 |
当C=120°时，根据余弦定理可得 c2=32+82-2×3×8cos120°=85，∴c=
| 85 |
综上，C=60° 或120°，c=
| 61 |
| 85 |
点评：本题考查余弦定理的应用，根据三角函数的值求角，求出 C=60° 或120°，是解题的关键．
练习册系列答案
相关题目
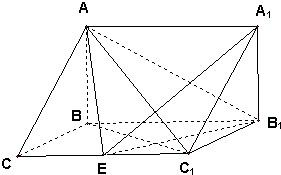如图，在三棱柱ABC-中，已知CC1=BB1=2，BC=1，
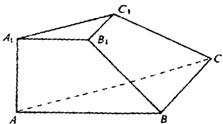如图，在三棱台A1B1C1-ABC中，已知A1A⊥底面ABC，A1A=A1B1=B1C1=a，B1B⊥BC，且B1B和底面ABC所成的角45°，求这个棱台的体积．
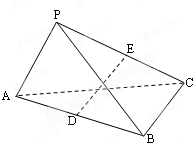（2012•姜堰市模拟）如图，在三棱锥P-ABC中，已知AB=AC=2，PA=1，∠PAB=∠PAC=∠BAC=60°，点D、E分别为AB、PC的中点．
（2010•聊城一模）如图，在三棱锥P-ABC中，已知PC⊥平面ABC，点C在平面PBA内的射影D在直线PB上．