题目内容
设0<x≤2,求函数y=4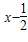 -3•2x+5的值域.
-3•2x+5的值域.
【答案】分析:换元,转化为二次函数,利用配方法,可求函数的值域.
解答:解:设2x=t,则
∵0<x≤2,∴t∈(1,4]
y=4 -3•2x+5=
-3•2x+5=
∵t∈(1,4],
∴t=3时,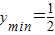 ;t=1时,
;t=1时,
∴函数的值域为 .
.
点评:本题考查复合函数的值域,考查换元法的运用,考查配方法,属于中档题.
解答:解:设2x=t,则
∵0<x≤2,∴t∈(1,4]
y=4
 -3•2x+5=
-3•2x+5=
∵t∈(1,4],
∴t=3时,
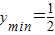 ;t=1时,
;t=1时,
∴函数的值域为
 .
.点评:本题考查复合函数的值域,考查换元法的运用,考查配方法,属于中档题.

练习册系列答案
相关题目
 的最小值
的最小值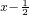 -3•2x+5的值域.
-3•2x+5的值域.