题目内容
已知椭圆C的焦点分别为F1(-2 ,0)和F2(2
,0)和F2(2 ,0),长轴长为6,设直线y=x+2交椭圆C于A、B两点.求:线段AB的中点坐标.
,0),长轴长为6,设直线y=x+2交椭圆C于A、B两点.求:线段AB的中点坐标.
【答案】分析:先求椭圆的方程,设椭圆C的方程为 +
+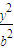 =1,根据条件可知a=3,c=2
=1,根据条件可知a=3,c=2 ,同时求得b=
,同时求得b=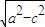 ,得到椭圆方程,由直线y=x+2交椭圆C于A、B两点,两方程联立,由韦达定理求得其中点坐标.
,得到椭圆方程,由直线y=x+2交椭圆C于A、B两点,两方程联立,由韦达定理求得其中点坐标.
解答:解:设椭圆C的方程为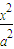 +
+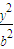 =1,
=1,
由题意a=3,c=2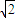 ,
,
b= =1.(3分)
=1.(3分)
∴椭圆C的方程为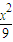 +y2=1.(5分)
+y2=1.(5分)
联立方程组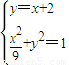 ,消y得10x2+36x+27=0,
,消y得10x2+36x+27=0,
因为该二次方程的判别式△>0,所以直线与椭圆有两个不同的交点,(9分)
设A(x1,y1),B(x2,y2),则x1+x2=-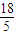 ,
,
故线段AB的中点坐标为(-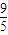 ,
,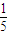 ).(12分)
).(12分)
点评:本题主要考查椭圆的性质及直线与椭圆的位置关系,要注意通性通法,即联立方程,看判别式,韦达定理的应用,同时也要注意一些细节,如相交与两点,要转化为判别式大于零来反映.
 +
+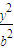 =1,根据条件可知a=3,c=2
=1,根据条件可知a=3,c=2 ,同时求得b=
,同时求得b=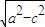 ,得到椭圆方程,由直线y=x+2交椭圆C于A、B两点,两方程联立,由韦达定理求得其中点坐标.
,得到椭圆方程,由直线y=x+2交椭圆C于A、B两点,两方程联立,由韦达定理求得其中点坐标.解答:解:设椭圆C的方程为
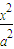 +
+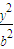 =1,
=1,由题意a=3,c=2
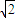 ,
,b=
 =1.(3分)
=1.(3分)∴椭圆C的方程为
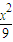 +y2=1.(5分)
+y2=1.(5分)联立方程组
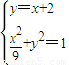 ,消y得10x2+36x+27=0,
,消y得10x2+36x+27=0,因为该二次方程的判别式△>0,所以直线与椭圆有两个不同的交点,(9分)
设A(x1,y1),B(x2,y2),则x1+x2=-
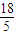 ,
,故线段AB的中点坐标为(-
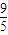 ,
,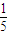 ).(12分)
).(12分)点评:本题主要考查椭圆的性质及直线与椭圆的位置关系,要注意通性通法,即联立方程,看判别式,韦达定理的应用,同时也要注意一些细节,如相交与两点,要转化为判别式大于零来反映.

练习册系列答案
 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案
相关题目