题目内容
若直线3x+4y+m=0与圆 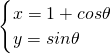 (θ为参数)至少有一个公共点,则实数m的取值范围是________.
(θ为参数)至少有一个公共点,则实数m的取值范围是________.
[-8,2]
分析:把圆的参数方程化为普通方程,找出圆心坐标与半径r,根据直线与圆至少有一个公共点,可知圆心到直线的距离d小于等于圆的半径r,利用点到直线的距离公式表示出d,即可列出关于m的绝对值不等式,分m+3大于等于0和小于0两种情况,分别根据绝对值的代数意义化简,即可求出m的取值范围.
解答:把圆的参数方程化为普通方程得:(x-1)2+y2=1,
所以圆心坐标为(1,0),半径r=1,
∵已知直线与圆至少有一个公共点,
∴圆心到直线的距离d=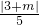 ≤r=1,
≤r=1,
化简得:|m+3|≤5,
当m+3≥0,即m≥-3时,不等式化为:m+3≤5,解得m≤2,
不等式的解集为:[-3,2];
当m+3<0,即m<-3时,不等式化为:-m-3≤5,解得m≥-8,
不等式的解集为:[-8,-3),
综上,实数m的取值范围是:[-8,2].
故答案为:[-8,2]
点评:此题考查了直线与圆的位置关系,点到直线的距离公式及绝对值不等式的解法;直线与圆的位置关系判断方法是:(d表示圆心到直线的距离,r表示圆的半径),当0≤d<r时,直线与圆相交;当d=r时,直线与圆位置关系为相切;当d>r时,直线与圆位置关系是相离.
分析:把圆的参数方程化为普通方程,找出圆心坐标与半径r,根据直线与圆至少有一个公共点,可知圆心到直线的距离d小于等于圆的半径r,利用点到直线的距离公式表示出d,即可列出关于m的绝对值不等式,分m+3大于等于0和小于0两种情况,分别根据绝对值的代数意义化简,即可求出m的取值范围.
解答:把圆的参数方程化为普通方程得:(x-1)2+y2=1,
所以圆心坐标为(1,0),半径r=1,
∵已知直线与圆至少有一个公共点,
∴圆心到直线的距离d=
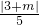 ≤r=1,
≤r=1,化简得:|m+3|≤5,
当m+3≥0,即m≥-3时,不等式化为:m+3≤5,解得m≤2,
不等式的解集为:[-3,2];
当m+3<0,即m<-3时,不等式化为:-m-3≤5,解得m≥-8,
不等式的解集为:[-8,-3),
综上,实数m的取值范围是:[-8,2].
故答案为:[-8,2]
点评:此题考查了直线与圆的位置关系,点到直线的距离公式及绝对值不等式的解法;直线与圆的位置关系判断方法是:(d表示圆心到直线的距离,r表示圆的半径),当0≤d<r时,直线与圆相交;当d=r时,直线与圆位置关系为相切;当d>r时,直线与圆位置关系是相离.

练习册系列答案
相关题目
已知两点M(-1,0),N(1,0)若直线3x-4y+m=0上存在点P满足
•
=0,则实数m的取值范围是( )
| PM |
| PN |
| A、(-∞,-5]∪[5,+∞) |
| B、(-∞,-25]∪[25,+∞) |
| C、[-25,25] |
| D、[-5,5] |
若直线3x+4y+m=0与圆
(θ为参数)相切,则实数m的值是( )
|
| A、10 | B、0 |
| C、10或0 | D、10或1 |
 (考生注意:请在下列三题中任选一题作答,如果多做,则按所做的第一题评分)
(考生注意:请在下列三题中任选一题作答,如果多做,则按所做的第一题评分)