题目内容
定义在[1,+∞)上的函数f(x)满足:①f(2x)=cf(x)(c为正常数);②当2≤x≤4时,f(x)=1-|x-3|.试解答下列问题:
(1)设c>2,方程f(x)=2的根由小到大依次记为a1,a2,a3,…,an,…,试证明:数列a2n-1+a2n为等比数列;
(2)①是否存在常数c,使函数的所有极大值点均落在同一条直线上?若存在,试求出c的所有取值并写出直线方程;若不存在,试说明理由;②是否存在常数c,使函数的所有极大值点均落在同一条以原点为顶点的抛物线上?若存在,试求出c的所有取值并写出抛物线方程;若不存在,试说明理由.
【答案】分析:(1)先利用分类讨论的方法化简函数f(x),令 ,从而n≥3,故
,从而n≥3,故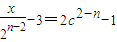 或
或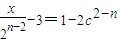 ,当n≥3时,
,当n≥3时,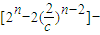
 =
=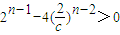 ,于是a1+a2=22+23,a3+a4=23+24,从而a2n-1+a2n=2n+1+2n+2=12•2n-1,n∈N*.从而得出数列a2n-1+a2n构成以12为首项,2为公比的等比数列.
,于是a1+a2=22+23,a3+a4=23+24,从而a2n-1+a2n=2n+1+2n+2=12•2n-1,n∈N*.从而得出数列a2n-1+a2n构成以12为首项,2为公比的等比数列.
(2)记函数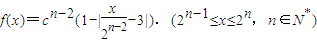 的极大值点为pn(xn,yn).由
的极大值点为pn(xn,yn).由 =
=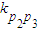 (k表示直线的斜率),得c=2或c=1.分别求出当c=2时的抛物线方程,以及当c=4,
(k表示直线的斜率),得c=2或c=1.分别求出当c=2时的抛物线方程,以及当c=4,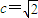 时,抛物线方程即可.
时,抛物线方程即可.
解答:解:函数f(x)是一个分段函数.
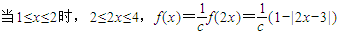 ;
;
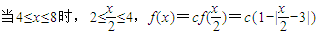 ;
;
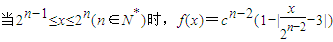 .
.
(1)令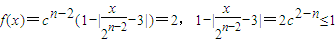 ,(2)
,(2)
从而n≥3,故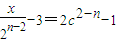 或
或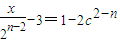 ,于是,
,于是,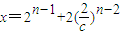 或
或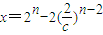 .
.
当n≥3时,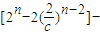
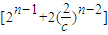 =
=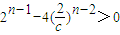
故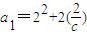 ,
,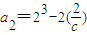 ,
,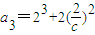 ,
,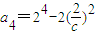 ,于是a1+a2=22+23,a3+a4=23+24,从而a2n-1+a2n=2n+1+2n+2=12•2n-1,n∈N*.
,于是a1+a2=22+23,a3+a4=23+24,从而a2n-1+a2n=2n+1+2n+2=12•2n-1,n∈N*.
故数列a2n-1+a2n构成以12为首项,2为公比的等比数列.(6分)
(2)记函数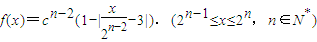 的极大值点为pn(xn,yn).
的极大值点为pn(xn,yn).
令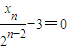 ,即xn=3•2n-2时,yn=cn-2,故pn(3•2n-2,cn-2).
,即xn=3•2n-2时,yn=cn-2,故pn(3•2n-2,cn-2).
分别令n=1,2,3得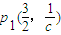 ,p2(3,1),p3(6,c).
,p2(3,1),p3(6,c).
由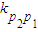 =
=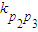 (k表示直线的斜率),得c=2或c=1.
(k表示直线的斜率),得c=2或c=1.
当c=2时,yn=2n-2,xn=3•2n-2,所有极大值点均在直线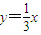 上;
上;
当c=1时,yn=1对n∈N*恒成立,此时极大值点均在直线y=1上.(10分)
以原点为顶点的抛物线方程可设为x2=py(p≠0)或y2=qx(q≠0).
若pn(3•2n-2,cn-2).在抛物线x2=py(p≠0)上,则(3•2n-2)2=pcn-2,
即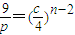 对n∈N*恒成立,从而c=4,p=9,抛物线方程为x2=9y;
对n∈N*恒成立,从而c=4,p=9,抛物线方程为x2=9y;
若pn(3•2n-2,cn-2).在抛物线y2=qx(q≠0)上,则(cn-2)2=3q•2n-2,
即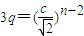 对n∈N*恒成立,从而
对n∈N*恒成立,从而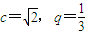 ,抛物线方程为y2=
,抛物线方程为y2= x(14分)
x(14分)
点评:本小题主要考查抛物线的标准方程、利用导数研究函数的极值、不等式的解法、数列与函数的综合等基础知识,考查运算求解能力、化归与转化思想.属于基础题.
 ,从而n≥3,故
,从而n≥3,故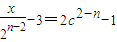 或
或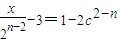 ,当n≥3时,
,当n≥3时,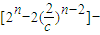
 =
=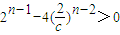 ,于是a1+a2=22+23,a3+a4=23+24,从而a2n-1+a2n=2n+1+2n+2=12•2n-1,n∈N*.从而得出数列a2n-1+a2n构成以12为首项,2为公比的等比数列.
,于是a1+a2=22+23,a3+a4=23+24,从而a2n-1+a2n=2n+1+2n+2=12•2n-1,n∈N*.从而得出数列a2n-1+a2n构成以12为首项,2为公比的等比数列.(2)记函数
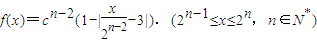 的极大值点为pn(xn,yn).由
的极大值点为pn(xn,yn).由 =
=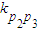 (k表示直线的斜率),得c=2或c=1.分别求出当c=2时的抛物线方程,以及当c=4,
(k表示直线的斜率),得c=2或c=1.分别求出当c=2时的抛物线方程,以及当c=4,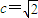 时,抛物线方程即可.
时,抛物线方程即可.解答:解:函数f(x)是一个分段函数.
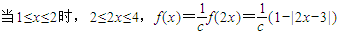 ;
;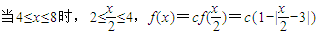 ;
;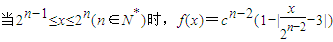 .
.(1)令
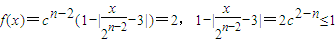 ,(2)
,(2)从而n≥3,故
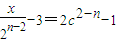 或
或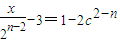 ,于是,
,于是,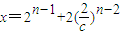 或
或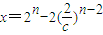 .
.当n≥3时,
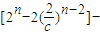
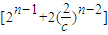 =
=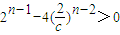
故
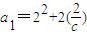 ,
,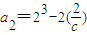 ,
,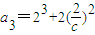 ,
,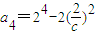 ,于是a1+a2=22+23,a3+a4=23+24,从而a2n-1+a2n=2n+1+2n+2=12•2n-1,n∈N*.
,于是a1+a2=22+23,a3+a4=23+24,从而a2n-1+a2n=2n+1+2n+2=12•2n-1,n∈N*.故数列a2n-1+a2n构成以12为首项,2为公比的等比数列.(6分)
(2)记函数
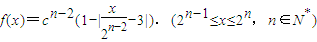 的极大值点为pn(xn,yn).
的极大值点为pn(xn,yn).令
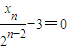 ,即xn=3•2n-2时,yn=cn-2,故pn(3•2n-2,cn-2).
,即xn=3•2n-2时,yn=cn-2,故pn(3•2n-2,cn-2).分别令n=1,2,3得
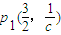 ,p2(3,1),p3(6,c).
,p2(3,1),p3(6,c).由
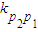 =
=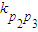 (k表示直线的斜率),得c=2或c=1.
(k表示直线的斜率),得c=2或c=1.当c=2时,yn=2n-2,xn=3•2n-2,所有极大值点均在直线
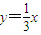 上;
上;当c=1时,yn=1对n∈N*恒成立,此时极大值点均在直线y=1上.(10分)
以原点为顶点的抛物线方程可设为x2=py(p≠0)或y2=qx(q≠0).
若pn(3•2n-2,cn-2).在抛物线x2=py(p≠0)上,则(3•2n-2)2=pcn-2,
即
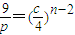 对n∈N*恒成立,从而c=4,p=9,抛物线方程为x2=9y;
对n∈N*恒成立,从而c=4,p=9,抛物线方程为x2=9y;若pn(3•2n-2,cn-2).在抛物线y2=qx(q≠0)上,则(cn-2)2=3q•2n-2,
即
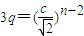 对n∈N*恒成立,从而
对n∈N*恒成立,从而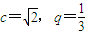 ,抛物线方程为y2=
,抛物线方程为y2= x(14分)
x(14分)点评:本小题主要考查抛物线的标准方程、利用导数研究函数的极值、不等式的解法、数列与函数的综合等基础知识,考查运算求解能力、化归与转化思想.属于基础题.

练习册系列答案
相关题目
设f(x)是定义在[1+a,2]上偶函数,则f(x)=ax2+bx-2在区间[0,2]上是( )
| A、增函数 | B、先增后减函数 | C、减函数 | D、与a,b有关,不能确定 |
设f(x)=ax2+bx+2是定义在[1+a,2]上的偶函数,则f(x)的值域是( )
| A、[-10,2] | B、[-12,0] | C、[-12,2] | D、与a,b有关,不能确定 |