题目内容
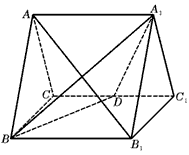
如图,正三棱柱ABC-A1B1C1的所有棱长都为2,D为CC1中点,
(Ⅰ)求证:AB1⊥平面A1BD;
(Ⅱ)求二面角A-A1D-B的大小。
(Ⅰ)求证:AB1⊥平面A1BD;
(Ⅱ)求二面角A-A1D-B的大小。
|
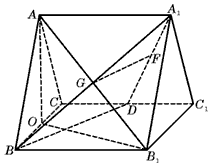
解:(Ⅰ)取BC中点O,连结AO, |
 |

练习册系列答案
相关题目
 如图,正三棱柱ABC-A1B1C1的各棱长都2,E,F分别是AB,A1C1的中点,则EF的长是( )
如图,正三棱柱ABC-A1B1C1的各棱长都2,E,F分别是AB,A1C1的中点,则EF的长是( )| A、2 | ||
B、
| ||
C、
| ||
D、
|
题目内容

|
解:(Ⅰ)取BC中点O,连结AO, |
 |

 如图,正三棱柱ABC-A1B1C1的各棱长都2,E,F分别是AB,A1C1的中点,则EF的长是( )
如图,正三棱柱ABC-A1B1C1的各棱长都2,E,F分别是AB,A1C1的中点,则EF的长是( )| A、2 | ||
B、
| ||
C、
| ||
D、
|