题目内容
已知函数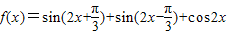
(1)求函数f(x)的最小正周期;
(2)将函数f(x)的图象沿向量
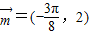 平移得到函数g(x)的图象,求函数g(x)在x∈[0,π]上的单调递减区间.
平移得到函数g(x)的图象,求函数g(x)在x∈[0,π]上的单调递减区间.
【答案】分析:(1)先对函数解析式利用三角公式进行化简整理得f(x)=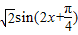 ,再直接代入周期计算公式即可;
,再直接代入周期计算公式即可;
(2)先根据函数图象的平移规律得到函数g(x)的解析式;再结合正弦函数的单调区间即可求解.
解答:解: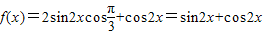 =
=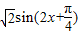 …(4分)
…(4分)
(1)函数f(x)的最小正周期为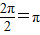 …(6分)
…(6分)
(2)由题意知g(x)=f(x+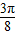 )+2=
)+2=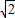 sin(2x+
sin(2x+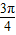 +
+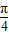 )+2=
)+2=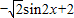 …(8分)
…(8分)
∵0≤x≤π∴0≤2x≤2π
由g(x)在[0,π]上单调递减
∴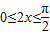 ,或
,或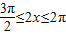
∵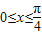 ,或
,或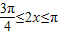 …(11分)
…(11分)
故函数f(x)的单调递减区间为[0,π]和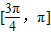 …(12分)
…(12分)
点评:本题主要考查三角函数的周期性以及正弦函数单调性的应用,属于对基础知识的考查,考查计算能力和整体思想.
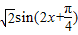 ,再直接代入周期计算公式即可;
,再直接代入周期计算公式即可;(2)先根据函数图象的平移规律得到函数g(x)的解析式;再结合正弦函数的单调区间即可求解.
解答:解:
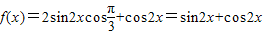 =
=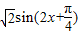 …(4分)
…(4分)(1)函数f(x)的最小正周期为
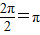 …(6分)
…(6分)(2)由题意知g(x)=f(x+
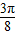 )+2=
)+2=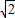 sin(2x+
sin(2x+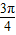 +
+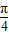 )+2=
)+2=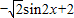 …(8分)
…(8分)∵0≤x≤π∴0≤2x≤2π
由g(x)在[0,π]上单调递减
∴
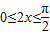 ,或
,或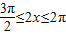
∵
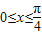 ,或
,或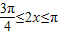 …(11分)
…(11分)故函数f(x)的单调递减区间为[0,π]和
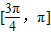 …(12分)
…(12分)点评:本题主要考查三角函数的周期性以及正弦函数单调性的应用,属于对基础知识的考查,考查计算能力和整体思想.

练习册系列答案
相关题目



 的极值点;
的极值点; 过点(0,—1),并且与曲线
过点(0,—1),并且与曲线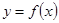 相切,求直线
相切,求直线 ,其中
,其中 ,求函数
,求函数 在
在 上的最小值.(其中e为自然对数的底数)
上的最小值.(其中e为自然对数的底数)