题目内容
二次函数y=ax2+bx+c(x∈R)的部分对应值如下表:
x | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 |
y | 6 | 0 | -4 | -6 | -6 | -4 | 0 | 6 |
则不等式ax2+bx+c>0的解集是 .
{x|x<-2或x>3}
解析:将点(0,-6),(1,-6),(2,-4)代入y=ax2+bx+c,得
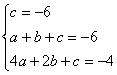
![]()
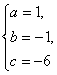 ?
?
不等式化为x2-x-6>0,即(x-3)(x+2)>0.
∴原不等式的解集为{x|x<-2或x>3}.

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目
题目内容
二次函数y=ax2+bx+c(x∈R)的部分对应值如下表:
x | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 |
y | 6 | 0 | -4 | -6 | -6 | -4 | 0 | 6 |
则不等式ax2+bx+c>0的解集是 .
{x|x<-2或x>3}
解析:将点(0,-6),(1,-6),(2,-4)代入y=ax2+bx+c,得
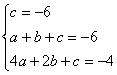
![]()
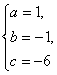 ?
?
不等式化为x2-x-6>0,即(x-3)(x+2)>0.
∴原不等式的解集为{x|x<-2或x>3}.

 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案