题目内容
给出下列四个命题:
①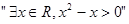 的否定是
的否定是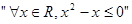 ;
;
②对于任意实数x,有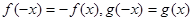 ,且
,且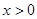 时,
时,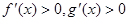 , 则
, 则 时,
时,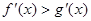
③函数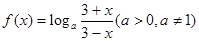 是偶函数;
是偶函数;
④若对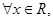 函数f(x)满足
函数f(x)满足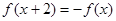 ,则4是该函数的一个周期,其中真命题的个数为
,则4是该函数的一个周期,其中真命题的个数为
①
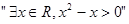 的否定是
的否定是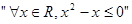 ;
;②对于任意实数x,有
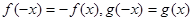 ,且
,且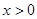 时,
时,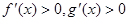 , 则
, 则 时,
时,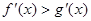
③函数
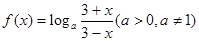 是偶函数;
是偶函数;④若对
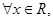 函数f(x)满足
函数f(x)满足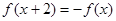 ,则4是该函数的一个周期,其中真命题的个数为
,则4是该函数的一个周期,其中真命题的个数为 3
此题考查命题的真假的判断;对①考查全称命题和特称命题的的否定,全称命题的否定是特称命题,特称命题的否定是全称命题。对于全称命题和特称命题的否定,首先把全称量词改为存在量词,把存在量词改为全称量词,然后在把结论否定,所以①正确;对②,因为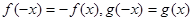 ,所以
,所以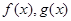 分别是奇函数和偶函数,而且由已知条件得到:当
分别是奇函数和偶函数,而且由已知条件得到:当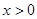 时,
时,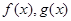 都是增函数,根据奇函数在对称区间上单调性相同,偶函数在对称区间上单调性相反,所以当
都是增函数,根据奇函数在对称区间上单调性相同,偶函数在对称区间上单调性相反,所以当 时,
时,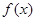 递增,所以
递增,所以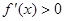 ;当
;当 时
时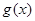 递减,所以
递减,所以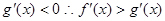 ;所以②正确;对③,判断函数的奇偶性,首先要求出函数的定义域,如果关于原点对称,在判断
;所以②正确;对③,判断函数的奇偶性,首先要求出函数的定义域,如果关于原点对称,在判断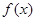 和
和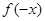 之间关系,此题中由
之间关系,此题中由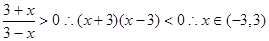 ,且
,且
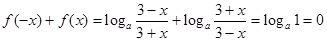 ,所以函数
,所以函数
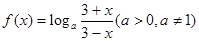 是奇函数,所以③错误;对于④,由已知得到
是奇函数,所以③错误;对于④,由已知得到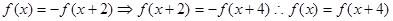 ,所以函数的最小正周期是4,所以④正确,所以正确的有3个;
,所以函数的最小正周期是4,所以④正确,所以正确的有3个;
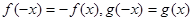 ,所以
,所以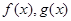 分别是奇函数和偶函数,而且由已知条件得到:当
分别是奇函数和偶函数,而且由已知条件得到:当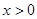 时,
时,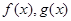 都是增函数,根据奇函数在对称区间上单调性相同,偶函数在对称区间上单调性相反,所以当
都是增函数,根据奇函数在对称区间上单调性相同,偶函数在对称区间上单调性相反,所以当 时,
时,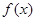 递增,所以
递增,所以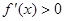 ;当
;当 时
时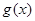 递减,所以
递减,所以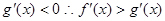 ;所以②正确;对③,判断函数的奇偶性,首先要求出函数的定义域,如果关于原点对称,在判断
;所以②正确;对③,判断函数的奇偶性,首先要求出函数的定义域,如果关于原点对称,在判断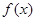 和
和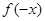 之间关系,此题中由
之间关系,此题中由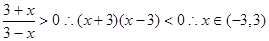 ,且
,且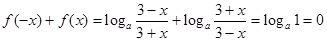 ,所以函数
,所以函数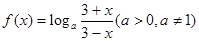 是奇函数,所以③错误;对于④,由已知得到
是奇函数,所以③错误;对于④,由已知得到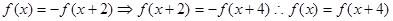 ,所以函数的最小正周期是4,所以④正确,所以正确的有3个;
,所以函数的最小正周期是4,所以④正确,所以正确的有3个;
练习册系列答案
相关题目
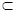 α,b
α,b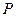 :对任意实数
:对任意实数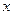 都有
都有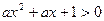 恒成立;
恒成立; :关于
:关于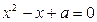 有实数根;如果
有实数根;如果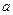 的取值范围.
的取值范围.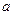 、
、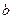 和不同的平面
和不同的平面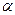 、
、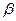 、
、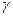 ,给出下列三个命题:
,给出下列三个命题: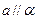 ,
,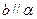 ,则
,则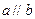 ②若
②若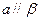 ,则
,则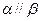
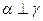 ,
,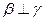 ,则
,则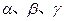 是三个不同的平面,则下列命题中的真命题是( )
是三个不同的平面,则下列命题中的真命题是( )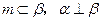 ,则
,则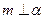
 ,
,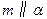 ,则
,则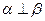
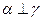 ,
,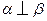 ,则
,则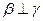
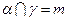 ,
,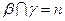 ,
,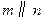 ,则
,则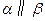
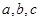 ,在下列命题中,真命题的是 ( )
,在下列命题中,真命题的是 ( )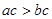 ”是“
”是“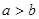 ”的必要条件;
”的必要条件;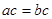 ”是“
”是“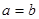 ”的必要条件;
”的必要条件;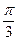 ,则△ABC必为锐角三角形;
,则△ABC必为锐角三角形;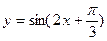 的图象向右平移
的图象向右平移