题目内容
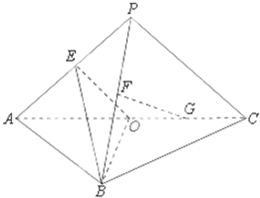 如图,平面PAC⊥平面ABC,点E、F、O分别为线段PA、PB、AC的中点,点G是线段CO的中点,AB=BC=AC=4,PA=PC=2
如图,平面PAC⊥平面ABC,点E、F、O分别为线段PA、PB、AC的中点,点G是线段CO的中点,AB=BC=AC=4,PA=PC=2| 2 |
求证:
(1)PA⊥平面EBO;
(2)FG∥平面EBO;
(3)求三棱锥E-PBC的体积.
分析:(1)先证明BO⊥面PAC,可得BO⊥PA.由OE∥PC,PC⊥PA 可得OE⊥PA,从而证得PA⊥平面EBO.
(2)由线段长度间的关系证明FG∥QO,进而证得FG∥平面EBO.
(3)先确定棱锥的高BO,求出BO的大小,然后求出底面PEC的大小,即可求解所求棱锥的体积.
(2)由线段长度间的关系证明FG∥QO,进而证得FG∥平面EBO.
(3)先确定棱锥的高BO,求出BO的大小,然后求出底面PEC的大小,即可求解所求棱锥的体积.
解答: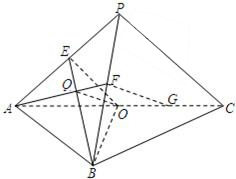 (1)证明:由题意可知,△PAC为等腰直角三角形,△ABC为等边三角形. 因为O为边AC的中点,所以BO⊥AC,
(1)证明:由题意可知,△PAC为等腰直角三角形,△ABC为等边三角形. 因为O为边AC的中点,所以BO⊥AC,
因为平面PAC⊥平面ABC,平面PAC∩平面ABC=AC,BO?平面ABC,所以,BO⊥面PAC.
因为PA?平面PAC,故 BO⊥PA.在等腰三角形PAC内,O,E为所在边的中点,故 OE∥PC,∴OE⊥PA,
又BO∩OE=O,所以,PA⊥平面EBO.
(2)证明:连AF交BE于Q,连QO.因为E、F、O分别为边PA、PB、PC的中点,
所以
=2. 又 Q是△PAB的重心.
于是,
=2=
,所以,FG∥QO.
因为FG?平面EBO,QO?平面EBO,所以,FG∥平面EBO.
(3)解:由(1)可知PA⊥平面EBO,所以PE⊥BO,
因为O是线段AC的中点,AB=BC=AC=4,所以BO⊥AC,
所以BO⊥平面PEC,BO是棱锥的高,BO=2
.
S△PEO=
S△PAC=
×
×4×
=2.
所以三棱锥E-PBC的体积V=
×2×2
=
.
 (1)证明:由题意可知,△PAC为等腰直角三角形,△ABC为等边三角形. 因为O为边AC的中点,所以BO⊥AC,
(1)证明:由题意可知,△PAC为等腰直角三角形,△ABC为等边三角形. 因为O为边AC的中点,所以BO⊥AC,因为平面PAC⊥平面ABC,平面PAC∩平面ABC=AC,BO?平面ABC,所以,BO⊥面PAC.
因为PA?平面PAC,故 BO⊥PA.在等腰三角形PAC内,O,E为所在边的中点,故 OE∥PC,∴OE⊥PA,
又BO∩OE=O,所以,PA⊥平面EBO.
(2)证明:连AF交BE于Q,连QO.因为E、F、O分别为边PA、PB、PC的中点,
所以
| AO |
| OG |
于是,
| AG |
| GF |
| AO |
| OG |
因为FG?平面EBO,QO?平面EBO,所以,FG∥平面EBO.
(3)解:由(1)可知PA⊥平面EBO,所以PE⊥BO,
因为O是线段AC的中点,AB=BC=AC=4,所以BO⊥AC,
所以BO⊥平面PEC,BO是棱锥的高,BO=2
| 3 |
S△PEO=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
(2
|
所以三棱锥E-PBC的体积V=
| 1 |
| 3 |
| 3 |
4
| ||
| 3 |
点评:本题考查直线与平面垂直的判定,棱柱、棱锥、棱台的体积,直线与平面平行的判定,考查空间想象能力,转化思想与计算能力.

练习册系列答案
相关题目
 倍,
倍,
 倍,
倍,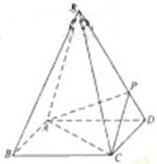 P为侧棱SD上的点。(Ⅰ)求证:AC⊥SD;
P为侧棱SD上的点。(Ⅰ)求证:AC⊥SD;