题目内容
已知命题p:方程a2x2+ax-2=0在[-1,1]上有且仅有一解.命题q:只有一个实数x满足不等式x2+2ax+2a≤0.若命题“p或q”是假命题,求a的取值范围.
分析:若命题p真,即方程a2x2+ax-2=0在[-1,1]上有且仅有一解,可求得-2<a≤-1或1≤a<2;若命题q真,即只有一个实数x满足不等式x2+2ax+2a≤0,由△=0可求得a=0或a=2,依题意,
命题p和命题q都是假命题,从而可求得a的取值范围.
命题p和命题q都是假命题,从而可求得a的取值范围.
解答:解:由a2x2+ax-2=0,得(ax+2)(ax-1)=0,显然a≠0,
∴x=-
或x=
,
∵方程a2x2+ax-2=0在[-1,1]上有且仅有一解,
故
或
∴-2<a≤-1或1≤a<2.
只有一个实数x满足不等式x2+2ax+2a≤0,
∴△=4a2-8a=0,解得a=0或a=2.
∵命题“p或q”是假命题,
∴命题p和命题q都是假命题,
∴a的取值范围为{a|a≤-2或-1<a<0或0<a<1或a>2}.
∴x=-
| 2 |
| a |
| 1 |
| a |
∵方程a2x2+ax-2=0在[-1,1]上有且仅有一解,
故
|
|
∴-2<a≤-1或1≤a<2.
只有一个实数x满足不等式x2+2ax+2a≤0,
∴△=4a2-8a=0,解得a=0或a=2.
∵命题“p或q”是假命题,
∴命题p和命题q都是假命题,
∴a的取值范围为{a|a≤-2或-1<a<0或0<a<1或a>2}.
点评:本题考查复合命题的真假,求得命题p真与命题q真中a的取值范围是关键,考查分析,理解与运算能力,属于中档题.

练习册系列答案
相关题目
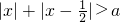 恒成立;若P或q为真,P且q为假,求实数a的取值范围.
恒成立;若P或q为真,P且q为假,求实数a的取值范围. 恒成立;若P或q为真,P且q为假,求实数a的取值范围.
恒成立;若P或q为真,P且q为假,求实数a的取值范围.