题目内容
等比数列{an}中，已知对任意自然数n，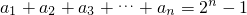
，则
=
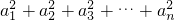- A.（2n-1）2
- B.
- C.4n-1
- D.
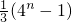
D
分析：由于Sn=a1+a2+…+an=2n-1，则可得a1=S1=1，an=Sn-Sn-1可求an，然后由等比数列的性质可知数列{
}是以q2为公比，以
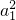为首项的等比数列，利用等比数列的求和公式可求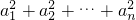
解答：设等比数列的公比为q，则由等比数列的性质可知数列{}是以q2为公比的等比数列
Sn=a1+a2+…+an=2n-1
∵a1=S1=1，an=Sn-Sn-1=2n-1-（2n-1-1）=2n-1适合n=1
∴
，
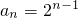则由等比数列的性质可知数列{}是以q2=4为公比，以1为首项的等比数列
∴=
=
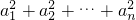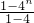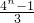
故选D
点评：本题主要考查了利用数列的递推公式
，等比数列的性质的应用，等比数列的求和公式的应用
分析：由于Sn=a1+a2+…+an=2n-1，则可得a1=S1=1，an=Sn-Sn-1可求an，然后由等比数列的性质可知数列{
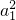}是以q2为公比，以为首项的等比数列，利用等比数列的求和公式可求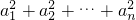解答：设等比数列的公比为q，则由等比数列的性质可知数列{
}是以q2为公比的等比数列Sn=a1+a2+…+an=2n-1
∵a1=S1=1，an=Sn-Sn-1=2n-1-（2n-1-1）=2n-1适合n=1
∴
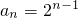，则由等比数列的性质可知数列{
}是以q2=4为公比，以1为首项的等比数列∴
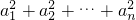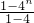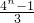
==故选D
点评：本题主要考查了利用数列的递推公式
，等比数列的性质的应用，等比数列的求和公式的应用 
练习册系列答案
中考解读考点精练系列答案
相关题目