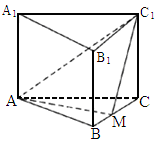
题目内容
(
唐山一中模拟)△ABC的BC边上的高为AD,BD=a,CD=b且a<b,将△ABC沿AD折成大小为θ的二面角B-AD-C,若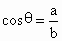 ,则三棱锥A-BDC的侧面△ABC是
,则三棱锥A-BDC的侧面△ABC是
[
]A
.锐角三角形B
.钝角三角形C
.直角三角形D
.形状与a,b的值有关的三角形
答案:C
解析:
解析:
|
由题意知∠ BDC=θ,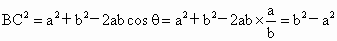 ,即 ,即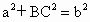 ,BC⊥BD,由三垂线定理得BC⊥AB,则三棱锥A-BDC的侧面△ABC是直角三角形,故选C. ,BC⊥BD,由三垂线定理得BC⊥AB,则三棱锥A-BDC的侧面△ABC是直角三角形,故选C. |

练习册系列答案
 优等生题库系列答案
优等生题库系列答案
相关题目
(
唐山一中模拟)设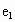 ,
,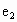 分别为具有公共焦点
分别为具有公共焦点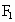 与
与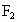 的椭圆和双曲线的离心率,P为两曲线的一个公共点,且满足
的椭圆和双曲线的离心率,P为两曲线的一个公共点,且满足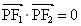 ,则
,则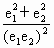 的值为
的值为
[
]|
A .1 |
B .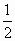 |
|
C .2 |
D .不确定 |
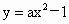 和点A(0,0),B(2,3),若抛物线和线段AB有且仅有一个公共点,则实数a的取值范围为__________.
和点A(0,0),B(2,3),若抛物线和线段AB有且仅有一个公共点,则实数a的取值范围为__________.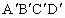 中,棱长为1,E、F分别是BC、CD上的点,且BE=CF=a(0<a<1),则
中,棱长为1,E、F分别是BC、CD上的点,且BE=CF=a(0<a<1),则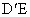 与
与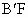 的位置关系是
的位置关系是
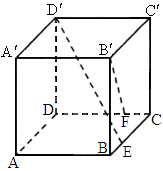
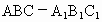 的底面边长为a,点M在BC上,△
的底面边长为a,点M在BC上,△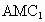 是以点M为直角顶点的等腰直角三角形.
是以点M为直角顶点的等腰直角三角形.
 的大小.
的大小.