题目内容
设a为实数,函数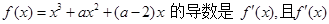 是偶函数,则曲线
是偶函数,则曲线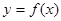 在原点处的切线方程为( )
在原点处的切线方程为( )
A.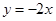 | B.y=3x | C.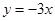 | D.y=4x |
A
解析试题分析:因为,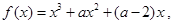
所以,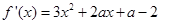 ,
,
又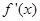 是偶函数,所以,a=0.即
是偶函数,所以,a=0.即
曲线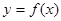 在原点处的切线斜率为-2,由直线方程的点斜式,整理得,曲线
在原点处的切线斜率为-2,由直线方程的点斜式,整理得,曲线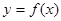 在原点处的切线方程为
在原点处的切线方程为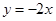 ,选A。
,选A。
考点:函数的奇偶性,导数的几何意义。
点评:小综合题,本题综合性较强,综合考查函数的奇偶性、导数的计算、导数的几何意义、直线方程的点斜式等。

练习册系列答案
相关题目
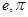 分别是自然对数的底和圆周率,则下列不等式不成立的是( )
分别是自然对数的底和圆周率,则下列不等式不成立的是( )
A.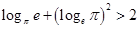 | B.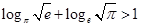 |
C.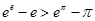 | D.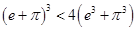 |
曲线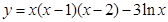 在点
在点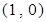 处的切线方程为( )
处的切线方程为( )
A.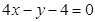 | B.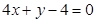 |
C. | D.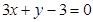 |
设函数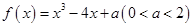 有三个零点
有三个零点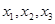 ,且
,且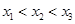 则下列结论正确的是( )
则下列结论正确的是( )
A.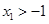 | B.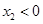 | C.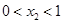 | D.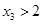 |
已知二次函数 的导数
的导数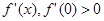 ,且
,且 的值域为
的值域为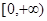 ,则
,则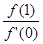 的最小值为( )
的最小值为( )
| A.3 | B.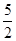 | C.2 | D.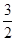 |
对于R上的可导的任意函数 ,若满足
,若满足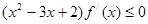 ,则函数
,则函数 在区间
在区间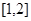 上必有( )
上必有( )
A. | B.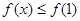 |
C.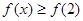 | D.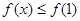 或 或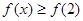 |
“函数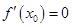 ”是“可导函数
”是“可导函数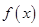 在点
在点 处取到极值”的 条件。 ( )
处取到极值”的 条件。 ( )
| A.充分不必要 | B.必要不充分 | C.充要 | D.既不充分也不必要 |
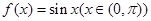 及直线
及直线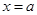 (
(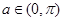 )与x轴围成,向矩形OABC内随机投掷一点,若落在阴影部分的概率为
)与x轴围成,向矩形OABC内随机投掷一点,若落在阴影部分的概率为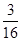 ,则
,则 的值为( )
的值为( )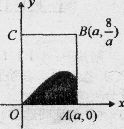
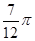
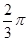
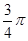
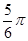
 具有下列特征:
具有下列特征: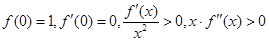 ,则
,则