题目内容
（理科）已知向量
=（sin2
x，cos2
x），
=（sin2
x，-cos2
x），g（x）=
•
．
（Ⅰ）求函数g（x）的解析式，并求其单调增区间；
（Ⅱ）若集合M={f（x）丨f（x）+f（x+2）=f（x+1），x∈R}，试判断g（x）与集合M的关系．
| a |
| π |
| 6 |
| π |
| 6 |
| b |
| π |
| 6 |
| π |
| 6 |
| a |
| b |
（Ⅰ）求函数g（x）的解析式，并求其单调增区间；
（Ⅱ）若集合M={f（x）丨f（x）+f（x+2）=f（x+1），x∈R}，试判断g（x）与集合M的关系．
分析：（Ⅰ）利用两个向量的数量积公式、二倍角公式求得g（x）=
•
=-cos
，令 2kπ≤
≤2kπ+π，k∈z，求得x的范围，可得g（x）的单调增区间．
（Ⅱ）利用两角和差的三角公式化简g（x）+g（x+2）=-cos
（x+1）=g（x+1），可得g（x）∈M．
| a |
| b |
| πx |
| 3 |
| πx |
| 3 |
（Ⅱ）利用两角和差的三角公式化简g（x）+g（x+2）=-cos
| π |
| 3 |
解答：解：（Ⅰ）由题意可得g（x）=
•
=sin4
-cos4
=sin2
-cos2
=-cos
，
故本题即求cos
得减区间．
令 2kπ≤
≤2kπ+π，k∈z，求得 6k≤x≤6k+3，k∈z．
故g（x）的单调增区间为[6k，6k+3]，k∈z．
（Ⅱ）由于g（x）+g（x+2）=-cos
-cos
(x+2)
=-cos
-cos
cos
+sin
sin
=-
cos
+
sin
，
=-cos
（x+1）=g（x+1），
∴g（x）∈M．
| a |
| b |
| πx |
| 6 |
| πx |
| 6 |
| πx |
| 6 |
| πx |
| 6 |
| πx |
| 3 |
故本题即求cos
| πx |
| 3 |
令 2kπ≤
| πx |
| 3 |
故g（x）的单调增区间为[6k，6k+3]，k∈z．
（Ⅱ）由于g（x）+g（x+2）=-cos
| πx |
| 3 |
| π |
| 3 |
=-cos
| πx |
| 3 |
| πx |
| 3 |
| 2π |
| 3 |
| πx |
| 3 |
| 2π |
| 3 |
| 1 |
| 2 |
| πx |
| 3 |
| ||
| 2 |
| πx |
| 3 |
=-cos
| π |
| 3 |
∴g（x）∈M．
点评：本题主要考查两个向量的数量积公式、余弦函数的单调区间，两角和差的三角公式省委应用，属于中档题
练习册系列答案
相关题目
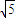）且方向向量为
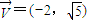的直线l交椭圆C于A、B两点，交x轴于M点，又
．
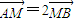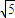）且方向向量为
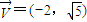的直线l交椭圆C于A、B两点，交x轴于M点，又
．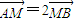