题目内容
三棱锥A-BCD内接于球0,BC=AD=2| 3 |
| π |
| 2 |
分析:首先确定球心的位置,根据直角三角形的勾股定理求出球的半径,找出最短距离是M的路径是A→B→C→D→A,根据直角三角形的性质知∠AOB=60°,∠AOD=120°,∠BOC=120°,∠COD=60°,M沿着这个路径,在球面上走大圆,刚好走过一个大圆,得到结果.
解答:解:设球0的半径为r,设E为直角三角形BCD的斜边BD的中点,
则E为过△BCD的小圆的圆心,根据直角三角形的性质知E是BD中点,
∴0E⊥面BCD,直角三角形0ED中,由勾股定理得 0D=r=2
∵∠BAD=∠BCD=
,
∴M的路径是A→B→C→D→A,
根据直角三角形的性质知∠AOB=60°,∠AOD=120°,∠BOC=120°,∠COD=60°
∴M沿着这个路径,在球面上走大圆,刚好走过一个大圆,
∴最短路径是4π
故答案为:4π
则E为过△BCD的小圆的圆心,根据直角三角形的性质知E是BD中点,
∴0E⊥面BCD,直角三角形0ED中,由勾股定理得 0D=r=2
∵∠BAD=∠BCD=
| π |
| 2 |
∴M的路径是A→B→C→D→A,
根据直角三角形的性质知∠AOB=60°,∠AOD=120°,∠BOC=120°,∠COD=60°
∴M沿着这个路径,在球面上走大圆,刚好走过一个大圆,
∴最短路径是4π
故答案为:4π
点评:本题考查多面体旋转体表面上的最短距离问题,考查直角三角形的性质,考查两点的球面最短距离是大圆的圆周,是一个综合题目.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
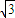 ,侧棱长为2,则球O的表面积为 .
,侧棱长为2,则球O的表面积为 .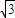 ,侧棱长为2,则球O的表面积为 .
,侧棱长为2,则球O的表面积为 . ,AB=CD=2且∠BAD=∠BCD=
,AB=CD=2且∠BAD=∠BCD= ,顶点A在面BCD上的射影恰在BD上,.一动点M从三棱锥的一个顶点出发沿球面运动,经过其它3个顶点后回到出发点,则动点M经过的最短距离为 .
,顶点A在面BCD上的射影恰在BD上,.一动点M从三棱锥的一个顶点出发沿球面运动,经过其它3个顶点后回到出发点,则动点M经过的最短距离为 .