题目内容
(1)已知两个等比数列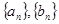 ,满足
,满足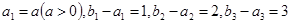 ,若数列
,若数列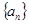 唯一,求
唯一,求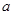 的值;
的值;
(2)是否存在两个等比数列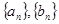 ,使得
,使得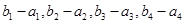 成公差不为
成公差不为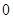 的等差数列?若存在,求
的等差数列?若存在,求 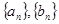 的通项公式;若不存在,说明理由.
的通项公式;若不存在,说明理由.
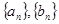 ,满足
,满足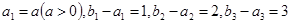 ,若数列
,若数列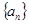 唯一,求
唯一,求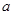 的值;
的值;(2)是否存在两个等比数列
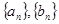 ,使得
,使得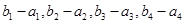 成公差不为
成公差不为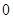 的等差数列?若存在,求
的等差数列?若存在,求 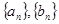 的通项公式;若不存在,说明理由.
的通项公式;若不存在,说明理由.(1)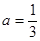
(2)不存在,见解析
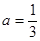
(2)不存在,见解析
解:(1)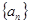 要唯一,
要唯一,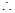 当公比
当公比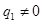 时,由
时,由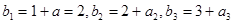 且
且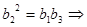
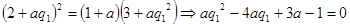 ,
,
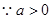 ,
,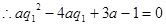 最少有一个根(有两个根时,保证仅有一个正根)
最少有一个根(有两个根时,保证仅有一个正根)
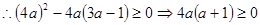 ,此时满足条件的a有无数多个,不符合。
,此时满足条件的a有无数多个,不符合。
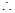 当公比
当公比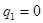 时,等比数列
时,等比数列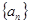 首项为a,其余各项均为常数0,唯一,此时由
首项为a,其余各项均为常数0,唯一,此时由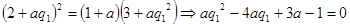 ,可推得
,可推得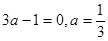 符合
符合
综上: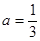 。
。
(2)假设存在这样的等比数列 ,则由等差数列的性质可得:
,则由等差数列的性质可得: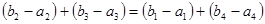 ,整理得:
,整理得: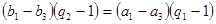
要使该式成立,则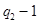 =
=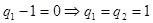 或
或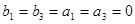 此时数列
此时数列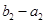 ,
,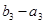 公差为0与题意不符,所以不存在这样的等比数列
公差为0与题意不符,所以不存在这样的等比数列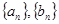 。
。
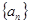 要唯一,
要唯一, 当公比
当公比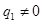 时,由
时,由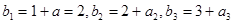 且
且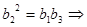
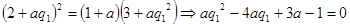 ,
, 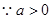 ,
,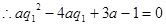 最少有一个根(有两个根时,保证仅有一个正根)
最少有一个根(有两个根时,保证仅有一个正根)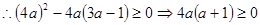 ,此时满足条件的a有无数多个,不符合。
,此时满足条件的a有无数多个,不符合。 当公比
当公比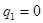 时,等比数列
时,等比数列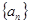 首项为a,其余各项均为常数0,唯一,此时由
首项为a,其余各项均为常数0,唯一,此时由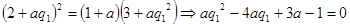 ,可推得
,可推得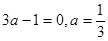 符合
符合综上:
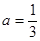 。
。(2)假设存在这样的等比数列
 ,则由等差数列的性质可得:
,则由等差数列的性质可得: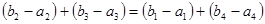 ,整理得:
,整理得: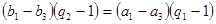
要使该式成立,则
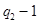 =
=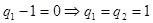 或
或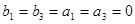 此时数列
此时数列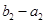 ,
,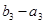 公差为0与题意不符,所以不存在这样的等比数列
公差为0与题意不符,所以不存在这样的等比数列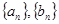 。
。
练习册系列答案
相关题目


 且
且 ,则
,则 ___________.
___________.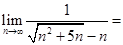 。
。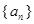 的前
的前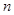 项和
项和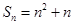
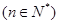 ,则
,则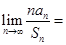 _______.
_______. 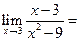
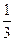
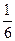
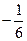
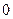
 .
.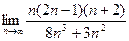 =_______。
=_______。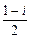 )n,(n∈N*),记Sn=|z2-z1|+|z3-z2|+…+|zn+1-zn|,则
)n,(n∈N*),记Sn=|z2-z1|+|z3-z2|+…+|zn+1-zn|,则 Sn=_________.
Sn=_________.