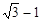题目内容
已知双曲线 上一点
上一点 ,过双曲线中心的直线交双曲线于
,过双曲线中心的直线交双曲线于 两点,记直线
两点,记直线 的斜率分别为
的斜率分别为 ,当
,当 最小时,双曲线离心率为( )
最小时,双曲线离心率为( )
A. B.
B. C
C D
D
B
解析试题分析:由题得,设点 ,由于点A,B为过原点的直线与双曲线的焦点,所以根据双曲线的对称性可得A,B关于原点对称,即
,由于点A,B为过原点的直线与双曲线的焦点,所以根据双曲线的对称性可得A,B关于原点对称,即 .则
.则 ,由于点A,C都在双曲线上,故有
,由于点A,C都在双曲线上,故有 ,两式相减得
,两式相减得
 .则
.则 ,对于函数
,对于函数 利用导数法可以得到当
利用导数法可以得到当 时,函数
时,函数 取得最小值.故当
取得最小值.故当 取得最小值时,
取得最小值时,  ,所以
,所以 ,故选B.
,故选B.
考点:导数 最值 双曲线 离心率

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
抛物线 的准线方程是
的准线方程是
A. | B. | C. | D.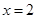 |
抛物线 的焦点坐标为( )
的焦点坐标为( )
A.(0, ) ) | B.( ,0) ,0) | C.(0,4) | D.(0,2) |
过(0,1)作直线,使它与抛物线 仅有一个公共点,这样的直线有( )条
仅有一个公共点,这样的直线有( )条
| A.1 | B.2 | C.3 | D.4 |
 的左、右焦点,过左焦点F1的直线
的左、右焦点,过左焦点F1的直线 与双曲线C的左、右两支分别交于A,B两点,若
与双曲线C的左、右两支分别交于A,B两点,若 ,则双曲线的离心率是( )
,则双曲线的离心率是( )


 和双曲线
和双曲线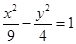 相交于A,B两点,线段AB的中点为M.设直线
相交于A,B两点,线段AB的中点为M.设直线

 =1的左、右两个焦点,若椭圆上满足PF1⊥PF2的点P有且只有两个,则离心率e的值为( )
=1的左、右两个焦点,若椭圆上满足PF1⊥PF2的点P有且只有两个,则离心率e的值为( )


 与
与 的曲线大致是( )
的曲线大致是( )
 分别是椭圆的左,右焦点,现以
分别是椭圆的左,右焦点,现以 为圆心作一个圆恰好经过椭圆中心并且交椭圆于点
为圆心作一个圆恰好经过椭圆中心并且交椭圆于点 ,若过
,若过 的直线
的直线 是圆
是圆