题目内容
一个透明密闭的正方体容器的棱长为1,该容器盛有一部分水的容积为V,经转动这个正方体,水面在容器中的形状可以是三角形,则正方体容器中水的容积V的范围是( )
分析:画出正方体,使其一个顶点放在桌面上,容易观察出何时取得最小值和最大值.
解答:解: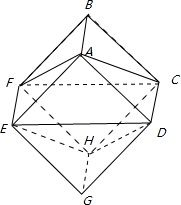 解:如图,正方体ABCD-EFGH,此时若要使液面为三角形,
解:如图,正方体ABCD-EFGH,此时若要使液面为三角形,
则液面必须低于平面EHD,或高于平面AFC.
而当平面EHD平行水平面放置时,若满足上述条件,则任意转动该正方体,
液面的形状都不可能是三角形.
所以液体体积必须<三棱柱G-EHD的体积
,
或者>正方体ABCD-EFGH体积-三棱柱B-AFC体积1-
=
,
即正方体容器中水的容积V的范围是( 0 ,
]∪[
, 1 )
故选D
 解:如图,正方体ABCD-EFGH,此时若要使液面为三角形,
解:如图,正方体ABCD-EFGH,此时若要使液面为三角形,则液面必须低于平面EHD,或高于平面AFC.
而当平面EHD平行水平面放置时,若满足上述条件,则任意转动该正方体,
液面的形状都不可能是三角形.
所以液体体积必须<三棱柱G-EHD的体积
| 1 |
| 6 |
或者>正方体ABCD-EFGH体积-三棱柱B-AFC体积1-
| 1 |
| 6 |
| 5 |
| 6 |
即正方体容器中水的容积V的范围是( 0 ,
| 1 |
| 6 |
| 5 |
| 6 |
故选D
点评:本题考查棱柱的结构特征,几何体的体积的求法,解题的关键是有着较强的空间感知能力,本题考查空间想象能力,及用公式计算的能力,是中档题.

练习册系列答案
 名校通行证有效作业系列答案
名校通行证有效作业系列答案
相关题目