题目内容
双曲线 的两个焦点为F1、F2,点P在双曲线上,若PF1⊥PF2,则点P到x轴的距离为 .
的两个焦点为F1、F2,点P在双曲线上,若PF1⊥PF2,则点P到x轴的距离为 .
【答案】分析:设出点P坐标(x,y),由PF1⊥PF2得到一个方程,将此方程代入双曲线的方程,消去x,求出|y|的值.
解答:解:设点P(x,y),
∵F1(-5,0)、F2(5,0),PF1⊥PF2,
∴ •
•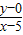 =-1,
=-1,
∴x2+y2=25 ①,
又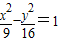 ,
,
∴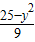 -
- =1,
=1,
∴y2=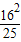 ,
,
∴|y|= ,
,
∴P到x轴的距离是 .
.
点评:本题考查双曲线的方程、性质的应用.
解答:解:设点P(x,y),
∵F1(-5,0)、F2(5,0),PF1⊥PF2,
∴
 •
•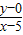 =-1,
=-1,∴x2+y2=25 ①,
又
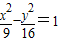 ,
,∴
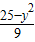 -
- =1,
=1,∴y2=
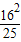 ,
,∴|y|=
 ,
,∴P到x轴的距离是
 .
.点评:本题考查双曲线的方程、性质的应用.

练习册系列答案
相关题目