题目内容
试求函数的值域f(x)=2x-3+| 13-4x |
分析:利用令
=t,将函数转化成关于t的二次函数求解.
| 13-4x |
解答:解:令
=t,t≥0,
∴x=
,
∴y=-
t2+t+
=-
(t-1)2+4≤ 4,当且仅当t=1时取等号
故所求函数的值域为 (-∞,4],
故值域为(-∞,4].
| 13-4x |
∴x=
| 13-t2 |
| 4 |
∴y=-
| 1 |
| 2 |
| 7 |
| 2 |
| 1 |
| 2 |
故所求函数的值域为 (-∞,4],
故值域为(-∞,4].
点评:本题通过换元将原函数转化为某个变量的二次函数,利用二次函数的最值,确定原函数的值域.换元法是一种重要的数学解题方法,掌握它的关键在于通过观察、联想,发现与构造出变换式(或新元换旧式、或新式换旧元、或新式换旧式).

练习册系列答案
相关题目
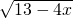 的值域?
的值域? .
. )为函数f(x)与g(x)的图象的公共点,试求实数α的值;
)为函数f(x)与g(x)的图象的公共点,试求实数α的值; 的值域.
的值域. 的值域?
的值域?