题目内容
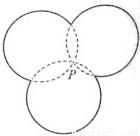
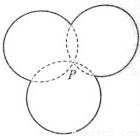
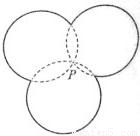
如图，图中的实线是由三段圆弧连接而成的一条封闭曲线C，各段弧所在的圆经过同一点P（点P不在C上）且半径相等．设第i段弧所对的圆心角为αi（i=1，2，3），则cos| α1 |
| 3 |
| α2+α3 |
| 3 |
| α1 |
| 3 |
| α2+α3 |
| 3 |
分析：根据cos（α+β）=cosαcosβ-sinαsinβ公式的逆运算得到cos
cos
-sin
sin
=cos
，由题意可知，α1+α2+α3=2π得到cos
=cos
=-
．
| α1 |
| 3 |
| α2+α3 |
| 3 |
| α1 |
| 3 |
| α2+α3 |
| 3 |
| α1+α2+α3 |
| 3 |
| α1+α2+α3 |
| 3 |
| 4π |
| 3 |
| 1 |
| 2 |
解答：解：cos
cos
-sin
sin
=cos
，方法
可令同过P点的三圆的交点分别是A，B，C，连接PA，PB，PC，可得得出∠APB+∠APC+∠BPC=2π
因为在各个圆的半径相等，故此三个角的大小都为
由于在圆中同弦所对的圆周角互补，故在各个圆中，AB，BC，CA所与三角相对的圆周角为
故AB，BC，CA所对的圆心角是
，
又α1+α2+α3=2π，所以cos
=-
．
故答案为：-
．
| α1 |
| 3 |
| α2+α3 |
| 3 |
| α1 |
| 3 |
| α2+α3 |
| 3 |
| α1+α2+α3 |
| 3 |
可令同过P点的三圆的交点分别是A，B，C，连接PA，PB，PC，可得得出∠APB+∠APC+∠BPC=2π
因为在各个圆的半径相等，故此三个角的大小都为
| 2π |
| 3 |
由于在圆中同弦所对的圆周角互补，故在各个圆中，AB，BC，CA所与三角相对的圆周角为
| π |
| 3 |
故AB，BC，CA所对的圆心角是
| 2π |
| 3 |
又α1+α2+α3=2π，所以cos
| α1+α2+α3 |
| 3 |
| 1 |
| 2 |
故答案为：-
| 1 |
| 2 |
点评：此题考查学生利用两角和与差的余弦函数的能力．
练习册系列答案
相关题目
= ．
= ．
= ．
= ．
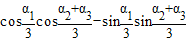
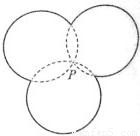
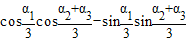
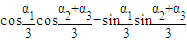
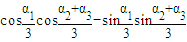