题目内容
(文科做)已知三棱锥S-ABC中,底面ABC为边长等于2的等边三角形,SA⊥底面ABC,SA=3,那么直线SB与平面SAC所成角的正弦值为( )
分析:过B作BD垂直于AC于D,连接SD,由已知中底面ABC为边长等于2的等边三角形,SA⊥底面ABC,易得∠BSD即为直线SB与平面SAC所成角,根据SA=3,使用勾股定理求出三角形SBD中各边的长后,解三角形SBD即可得到.
解答:解:过B作BD垂直于AC于D,连接SD
∵底面ABC为边长等于2的等边三角形,SA⊥底面ABC,
∴BD⊥AC,SA⊥BD,AC∩SA=A
则BD⊥平面SAC,
则∠BSD即为直线SB与平面SAC所成角
∵SA=3,
∴SD=
,BD=
,SB=
,
在Rt∠SBD中,sin∠BSD=
=
.
故选B.
∵底面ABC为边长等于2的等边三角形,SA⊥底面ABC,
∴BD⊥AC,SA⊥BD,AC∩SA=A
则BD⊥平面SAC,
则∠BSD即为直线SB与平面SAC所成角
∵SA=3,
∴SD=
| 10 |
| 3 |
| 13 |
在Rt∠SBD中,sin∠BSD=
| BD |
| SB |
| ||
| 13 |
故选B.
点评:本题考查的知知识点是直线与平面所成的角,其中求出直线与平面夹角的平面角,将线面夹角问题转化为解三角形问题是解答本题的关键.

练习册系列答案
 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案
相关题目
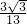
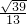
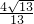
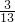
 (Ⅱ)求二面角M-BC'-B'的大小;
(Ⅱ)求二面角M-BC'-B'的大小;






