题目内容
某种产品的广告费用支出x(千元)与销售额y(10万元)之间有如下的对应数据:
(Ⅰ)请画出上表数据的散点图;
(Ⅱ)请根据上表提供的数据,用最小二乘法求出销售额y关于费用支出x的线性回归方程
=
x+
.
(III)当广告费用支出1万元时,预测一下该商品的销售额为多少万元?
(参考值:2×3+4×4+5×6+6×5+8×7=138,22+42+52+62+82=145)
| x | 2 | 4 | 5 | 6 | 8 |
| y | 3 | 4 | 6 | 5 | 7 |
(Ⅱ)请根据上表提供的数据,用最小二乘法求出销售额y关于费用支出x的线性回归方程
 |
| y |
 |
| b |
 |
| a |
(III)当广告费用支出1万元时,预测一下该商品的销售额为多少万元?
(参考值:2×3+4×4+5×6+6×5+8×7=138,22+42+52+62+82=145)
分析:(I)根据表中所给的五对数据,得到五个有序数对,在平面直角坐标系中画出点,得到散点图.
(II)先做出横标和纵标的平均数,得到这组数据的样本中心点,利用最小二乘法做出线性回归方程的系数,再做出a的值,协会粗线性回归方程.
(III)把所给的x的值代入线性回归方程,求出y的值,这里的y的值是一个预报值,或者说是一个估计值.
(II)先做出横标和纵标的平均数,得到这组数据的样本中心点,利用最小二乘法做出线性回归方程的系数,再做出a的值,协会粗线性回归方程.
(III)把所给的x的值代入线性回归方程,求出y的值,这里的y的值是一个预报值,或者说是一个估计值.
解答:解:(I)根据表中所给的五对数据,得到五个有序数对,在平面直角坐标系中画出点,得到散点图.
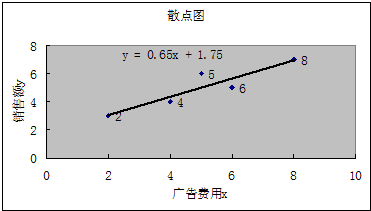
(II)∵
=
=5,
=
=5,
2×3+4×4+5×6+6×5+8×7=138,22+42+52+62+82=145
∴b=
=0.65
∴a=
-b
=5-0.65×5=1.75
∴回归直线方程为y=0.65x+1.75
(III)当x=1时,预报y的值为y=1×0.65+1.75=8.25.即销售额为8.25万元

(II)∵
. |
| x |
| 2+4+5+6+8 |
| 5 |
. |
| y |
| 30+40+60+50+70 |
| 5 |
2×3+4×4+5×6+6×5+8×7=138,22+42+52+62+82=145
∴b=
| |||||||
|
∴a=
. |
| y |
. |
| x |
∴回归直线方程为y=0.65x+1.75
(III)当x=1时,预报y的值为y=1×0.65+1.75=8.25.即销售额为8.25万元
点评:本题考查线性回归方程的求法和应用,本题解题的关键是看出这组变量是线性相关的,进而正确运算求出线性回归方程的系数,本题是一个基础题.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
某种产品的广告费用支出x(万元)与销售额y(万元)之间有如下的对应数据:
(1)画出散点图;
(2)求回归直线方程;
(3)据此估计广告费用为9万元时,销售收入y的值.
参考公式:回归直线的方程
=bx+a,其中b=
=
,a=
-b
.
| x | 2 | 4 | 5 | 6 | 8 |
| y | 30 | 40 | 60 | 50 | 70 |
(2)求回归直线方程;
(3)据此估计广告费用为9万元时,销售收入y的值.
参考公式:回归直线的方程
| ? |
| y |
| |||||
(yi-
|
| |||||||
|
. |
| y |
. |
| x |
某种产品的广告费用支出x万元与销售额y万元之间有如下的对应数据:
(1)画出上表数据的散点图;
(2)根据上表提供的数据,求出y关于x的线性回归方程;
(3)据此估计广告费用为10万元时,所得的销售收入.(参考数值:
xi2=145,
xiyi=1270,)
| x | 2 | 4 | 5 | 6 | 8 |
| y | 20 | 30 | 50 | 50 | 70 |
(2)根据上表提供的数据,求出y关于x的线性回归方程;
(3)据此估计广告费用为10万元时,所得的销售收入.(参考数值:
| 5 |
 |
| i=1 |
| 5 |
 |
| i=1 |