题目内容
已知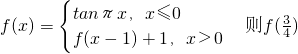 =________.
=________.
0
分析:分段函数在不同区间有不同对应法则,先将f( )转化为f(
)转化为f(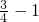 )+1,进而即可求出其函数值.
)+1,进而即可求出其函数值.
解答:∵ >0,∴f(
>0,∴f( )=f(
)=f(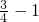 )+1=f(-
)+1=f(- )+1,
)+1,
又∵ <0,∴f(-
<0,∴f(- )=
)=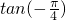 =-1,
=-1,
∴f( )=-1+1=0.
)=-1+1=0.
故答案为0.
点评:本题考查了分段函数求值,其关键是由自变量找对应区间.
分析:分段函数在不同区间有不同对应法则,先将f(
 )转化为f(
)转化为f(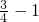 )+1,进而即可求出其函数值.
)+1,进而即可求出其函数值.解答:∵
 >0,∴f(
>0,∴f( )=f(
)=f(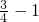 )+1=f(-
)+1=f(- )+1,
)+1,又∵
 <0,∴f(-
<0,∴f(- )=
)=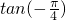 =-1,
=-1,∴f(
 )=-1+1=0.
)=-1+1=0.故答案为0.
点评:本题考查了分段函数求值,其关键是由自变量找对应区间.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
某地区为下岗人员免费提供财会和计算机培训,以提高下岗人员的再就业能力.每名下岗人员可以选择参加一项培训、参加两项培训或不参加培训,已知参加过财会培训的有60%,参加过计算机培训的有75%.假设每个人对培训项目的选择是相互独立的,且各人的选择相互之间没有影响.
(Ⅰ)任选1名下岗人员,求该人参加过培训的概率;
(Ⅱ)任选3名下岗人员,记ξ为3人中参加过培训的人数,求ξ的分布列和期望.
(Ⅰ)任选1名下岗人员,求该人参加过培训的概率;
(Ⅱ)任选3名下岗人员,记ξ为3人中参加过培训的人数,求ξ的分布列和期望.
| ξ | 0 | 1 | 2 | 3 |
| P | 0.021 | 0.027 | 0.243 | 0.729 |
已知函数f(x)=-x3+ax2-x-1在(-∞,+∞)上是单调函数,则实数a的取值范围是( )
A、(-∞,-
| ||||
B、[-
| ||||
C、(-∞,-
| ||||
D、(-
|
已知函数f(x)=
若f(2-a2)>f(a),则实数a的取值范围是( )
|
| A、(-∞,-1)∪(2,+∞) |
| B、(-1,2) |
| C、(-2,1) |
| D、(-∞,-2)∪(1,+∞) |