题目内容
若不等式a>|t-1|-|t-2|对任意t∈R恒成立,则函数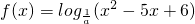 的单调递减区间为
的单调递减区间为
- A.
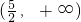
- B.(3,+∞)
- C.
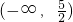
- D.(-∞,2)
B
分析:由不等式a>|t-1|-|t-2|对任意t∈R恒成立,知a>1.从而得到0< <1.由此能求出函数
<1.由此能求出函数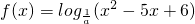 的单调递减区间.
的单调递减区间.
解答:设y=|t-1|-|t-2|,由t-1=0,得t=1;由t-2=0,得t=2.
当t≥2时,y=t-1-t+2=1;
当1≤t<2时,y=t-1-2+t=2t-3∈[-1,1);
当t<1时,y=1-t-2+t=-1.
∴y=|t-1|-|t-2|的值域是[-1,1].
∵不等式a>|t-1|-|t-2|对任意t∈R恒成立,∴a>1.∴0< <1.
<1.
∵函数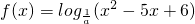 ,
,
∴x2-5x+6>0,解得x>3,或x<2.
∵m=x2-5x+6是开口向上,对称轴为x= 的抛物线,
的抛物线,
∴函数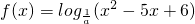 的单调递减区间为(3,+∞).
的单调递减区间为(3,+∞).
故选B.
点评:本题考查函数的单调减区间的求法,解题时要认真审题,仔细解答,注意绝对值的性质、对数函数性质和复合函数的单调等知识点的灵活运用.
分析:由不等式a>|t-1|-|t-2|对任意t∈R恒成立,知a>1.从而得到0<
 <1.由此能求出函数
<1.由此能求出函数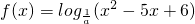 的单调递减区间.
的单调递减区间.解答:设y=|t-1|-|t-2|,由t-1=0,得t=1;由t-2=0,得t=2.
当t≥2时,y=t-1-t+2=1;
当1≤t<2时,y=t-1-2+t=2t-3∈[-1,1);
当t<1时,y=1-t-2+t=-1.
∴y=|t-1|-|t-2|的值域是[-1,1].
∵不等式a>|t-1|-|t-2|对任意t∈R恒成立,∴a>1.∴0<
 <1.
<1.∵函数
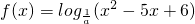 ,
,∴x2-5x+6>0,解得x>3,或x<2.
∵m=x2-5x+6是开口向上,对称轴为x=
 的抛物线,
的抛物线,∴函数
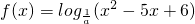 的单调递减区间为(3,+∞).
的单调递减区间为(3,+∞).故选B.
点评:本题考查函数的单调减区间的求法,解题时要认真审题,仔细解答,注意绝对值的性质、对数函数性质和复合函数的单调等知识点的灵活运用.

练习册系列答案
相关题目
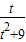 ≤a≤
≤a≤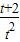 在t∈(0,2]上恒成立,则a的取值范围是( )
在t∈(0,2]上恒成立,则a的取值范围是( ) ,1]
,1]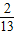 ,1]
,1] ,
,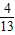 ]
] ,2
,2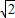 ]
]