题目内容
已知点P在圆x2+y2=1上运动,过点P作x轴的垂线,垂足为D,点M在DP的延长线上,且有|DP|=|MP|.(1)求M点的轨迹方程C;(2)已知直线l过点(0,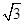 ),且斜率为1,求l与C相交所得的弦长.
),且斜率为1,求l与C相交所得的弦长.
【答案】
(1) x2 + =1
(2)
=1
(2) 
【解析】此题考查了直线与圆相交的性质,以及动点的轨迹方程,涉及的知识有:直线与圆的交点,一元二次方程根与系数的关系,两点间的距离公式,点到直线的距离公式,基本不等式的运用,以及直线与圆相切时,圆心到直线的距离等于圆的半径的性质,利用了转化及分类讨论的思想,是一道综合性较强的试题.
(1)设出M的坐标为(x,y),点P的坐标为(x0,y0),由题意DP⊥x轴,点M在DP的延长线上,且|DP|=|MP|,找出x0与x的关系及y0与y的关系,记作①,根据P在圆上,将P的坐标代入圆的方程,记作②,将①代入②,即可得到点M的轨迹方程;
(2)直线与圆联立求解方程组,结合根与系数的关系得到弦长公式。
解:(1)设P(x0,y0),M(x,y),由题意知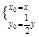 ,
……3分
,
……3分
又点P在圆x2+y2=1,可得M点的轨迹方程为x2 + =1. ……6分
=1. ……6分
(2)由(1)知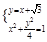 联立上式得4x2+(x+
联立上式得4x2+(x+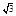 )2=4,5x2+2
)2=4,5x2+2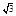 x-1=0,可知必有D>0…8分
x-1=0,可知必有D>0…8分
设l与C的交点为A(x1,y1), B(x2,y2),则有x1+x2 =- , x1x2
=-
, x1x2
=- .…10分
.…10分
\|AB|=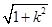 |x1-x2|=
|x1-x2|=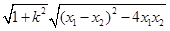
= =
= =
= . ……12分
. ……12分

练习册系列答案
相关题目
 ,则k=( )
,则k=( )