题目内容
已知椭圆 的离心率
的离心率 ,且直线
,且直线 是抛物线
是抛物线 的一条切线.
的一条切线.
(1)求椭圆的方程;
(2)点P  为椭圆上一点,直线
为椭圆上一点,直线 ,判断l与椭圆的位置关系并给出理由;
,判断l与椭圆的位置关系并给出理由;
(3)过椭圆上一点P作椭圆的切线交直线 于点A,试判断线段AP为直径的圆是否恒过定点,若是,求出定点坐标;若不是,请说明理由.
于点A,试判断线段AP为直径的圆是否恒过定点,若是,求出定点坐标;若不是,请说明理由.
(1)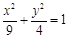 ;(2)相切;(3)定点
;(2)相切;(3)定点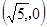
解析试题分析:(1)利用离心率 ,直线
,直线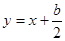 是抛物线
是抛物线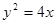 的一条切线,所以联立方程得到
的一条切线,所以联立方程得到 ,利用椭圆中
,利用椭圆中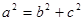 ,算出
,算出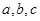 .求出方程.
.求出方程.
(2)直线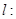
 与椭圆方程联立,注意用到平方相减消
与椭圆方程联立,注意用到平方相减消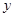 ,得到关于
,得到关于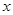 的方程,求其
的方程,求其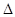 ,利用点
,利用点 在椭圆上的条件,判定直线与椭圆的位置关系;
在椭圆上的条件,判定直线与椭圆的位置关系;
3. 首先取两种特殊情形:切点分别在短轴两端点时,求其切线方程,并求他们的交点,交点有可能是恒过的定点,如果是圆上恒过的定点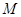 ,如果是则需满足,
,如果是则需满足,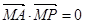 ,从而判定所求交点是否是真正的定点.此题属于较难习题.
,从而判定所求交点是否是真正的定点.此题属于较难习题.
试题解析:(1)因为直线 是抛物线
是抛物线 的一条切线,
的一条切线,
所以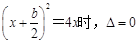 ,
,
即 2分
2分
又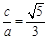 ,所以
,所以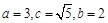 ,
,
所以椭圆的方程是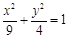 . 4分
. 4分
(2)由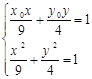
得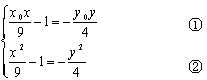
由①2+②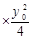 得
得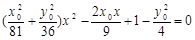
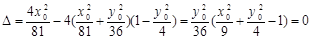
∴直线l与椭圆相切 8分
(3)首先取两种特殊情形:切点分别在短轴两端点时,
求得两圆的方程为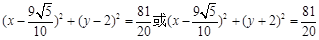 ,
,
两圆相交于点(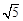 ,0),(
,0),(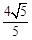 ,0),
,0),
若定点为椭圆的右焦点(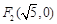 .
.
则需证: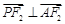 .设点
.设点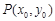 ,则椭圆过点P的切线方程是
,则椭圆过点P的切线方程是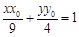 ,
,
所以点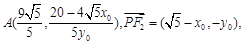
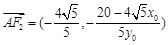 ,
,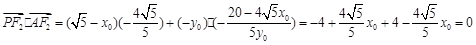 所以
所以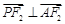 . 11分
. 11分
若定点为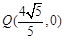 ,
,
则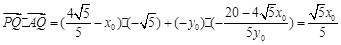 ,不满足题意.
,不满足题意.
综上,以线段AP为直径的圆恒过定点(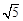 ,0). 13分
,0). 13分
考点:1.椭圆的性质与方程;2.直线与圆锥曲线相交时的综合问题.

练习册系列答案
相关题目
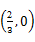 ,求曲线上距点A最近的点P的坐标及相应的距离|PA|.
,求曲线上距点A最近的点P的坐标及相应的距离|PA|.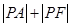 的最小值及此时P点的坐标.
的最小值及此时P点的坐标. 的两个焦点分别为
的两个焦点分别为 和
和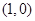 ,离心率
,离心率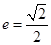 .
. (
(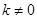 )与椭圆
)与椭圆 、
、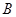 ,且线段
,且线段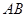
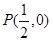 ,求实数
,求实数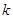 的取值范围.
的取值范围. 的离心率为
的离心率为 ,以原点为圆心、椭圆的短半轴长为半径的圆与直线
,以原点为圆心、椭圆的短半轴长为半径的圆与直线 相切.
相切. 的方程;
的方程; ,过点
,过点 作直线
作直线 (不与
(不与 轴重合)交椭圆于
轴重合)交椭圆于 、
、 两点,连结
两点,连结 、
、 分别交直线
分别交直线 于
于 、
、 两点,试探究直线
两点,试探究直线 、
、 的斜率之积是否为定值,若为定值,请求出;若不为定值,请说明理由.
的斜率之积是否为定值,若为定值,请求出;若不为定值,请说明理由.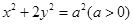 的一个顶点和两个焦点构成的三角形的面积为4.
的一个顶点和两个焦点构成的三角形的面积为4.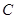 的方程;
的方程; 与椭圆
与椭圆 、
、 两点,试问,是否存在
两点,试问,是否存在 轴上的点
轴上的点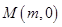 ,使得对任意的
,使得对任意的 ,
, 为定值,若存在,求出
为定值,若存在,求出 点的坐标,若不存在,说明理由.
点的坐标,若不存在,说明理由. 与抛物线
与抛物线 (常数
(常数 )相交于不同的两点
)相交于不同的两点 、
、 ,且
,且 (
( 为定值),线段
为定值),线段 的中点为
的中点为 ,与直线
,与直线 平行的切线的切点为
平行的切线的切点为 (不与抛物线对称轴平行或重合且与抛物线只有一个公共点的直线称为抛物线的切线,这个公共点为切点).
(不与抛物线对称轴平行或重合且与抛物线只有一个公共点的直线称为抛物线的切线,这个公共点为切点).
 、
、 表示出
表示出 垂直于
垂直于 轴;
轴; 的面积,证明
的面积,证明 、
、 ,再作与
,再作与 、
、 ,小张马上写出了
,小张马上写出了 、
、 的面积,由此小张求出了直线
的面积,由此小张求出了直线 与抛物线围成的面积,你认为小张能做到吗?请你说出理由.
与抛物线围成的面积,你认为小张能做到吗?请你说出理由.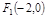 、
、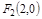 ,动点N满足
,动点N满足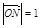 (O为坐标原点),
(O为坐标原点), ,
,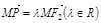 ,
,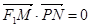 ,求点P的轨迹方程.
,求点P的轨迹方程. 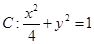 的上、下顶点分别为
的上、下顶点分别为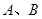 ,点
,点 在椭圆上,且异于点
在椭圆上,且异于点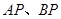 与直线
与直线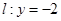 分别交于点
分别交于点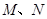 ,
,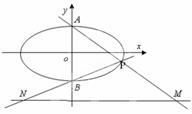
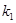 、
、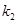 ,求证:
,求证: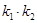 为定值;
为定值;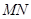 为直径的圆是否经过定点?请证明你的结论.
为直径的圆是否经过定点?请证明你的结论. .过点(m,0)作圆
.过点(m,0)作圆 的切线l交椭圆G于A,B两点.
的切线l交椭圆G于A,B两点. 表示为m的函数,并求
表示为m的函数,并求