题目内容
已知抛物线C:y2=2px(p>0),F为抛物线C的焦点,A为抛物线C上的动点,过A作抛物线准线l的垂线,垂足为Q.(1)若点P(0,2)与点F的连线恰好过点A,且∠PQF=90°,求抛物线方程;
(2)设点M(m,0)在x轴上,若要使∠MAF总为锐角,求m的取值范围.
【答案】分析:(1)先由题意知:|AQ|=|AF,再依据A为PF的中点且点A在抛物线上,求得p值,从而得出抛物线方程;
(2)设A(x,y),y2=2px,根据题意:∠MAF为锐角根据向量的数量积得出: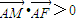 对x≥0都成立,令
对x≥0都成立,令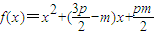 >0对x≥0都成立,下面结合二次函数的性质分类讨论,即可求得m的取值范围即可.
>0对x≥0都成立,下面结合二次函数的性质分类讨论,即可求得m的取值范围即可.
解答:解:(1)由题意知:|AQ|=|AF|,
∵∠PQF=90°,∴A为PF的中点,
∵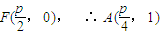 ,
,
且点A在抛物线上,代入得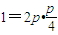 ⇒
⇒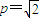
所以抛物线方程为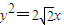 .…(5分)
.…(5分)
(2)设A(x,y),y2=2px,
根据题意:∠MAF为锐角 且
且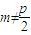 ,
,
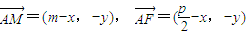 ,
, ,
,
∵y2=2px,所以得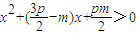 对x≥0都成立
对x≥0都成立
令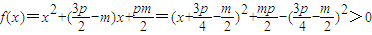
对x≥0都成立…(9分)
①若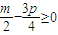 ,即
,即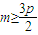 时,只要使
时,只要使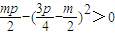 成立,
成立,
整理得: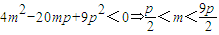 ,且
,且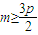 ,
,
所以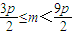 .…(11分)
.…(11分)
②若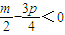 ,即
,即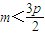 ,只要使
,只要使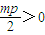 成立,得m>0
成立,得m>0
所以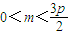 …(13分)
…(13分)
由①②得m的取值范围是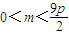 且
且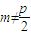 .…(15分)
.…(15分)
点评:本题主要考查了抛物线的标准方程、抛物线的简单性质,同时考查了向量的数量积,考查了计算能力.
(2)设A(x,y),y2=2px,根据题意:∠MAF为锐角根据向量的数量积得出:
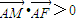 对x≥0都成立,令
对x≥0都成立,令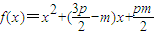 >0对x≥0都成立,下面结合二次函数的性质分类讨论,即可求得m的取值范围即可.
>0对x≥0都成立,下面结合二次函数的性质分类讨论,即可求得m的取值范围即可.解答:解:(1)由题意知:|AQ|=|AF|,
∵∠PQF=90°,∴A为PF的中点,
∵
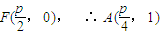 ,
,且点A在抛物线上,代入得
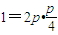 ⇒
⇒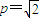
所以抛物线方程为
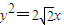 .…(5分)
.…(5分)(2)设A(x,y),y2=2px,
根据题意:∠MAF为锐角
 且
且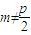 ,
,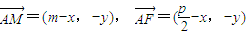 ,
, ,
,∵y2=2px,所以得
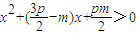 对x≥0都成立
对x≥0都成立令
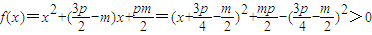
对x≥0都成立…(9分)
①若
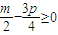 ,即
,即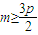 时,只要使
时,只要使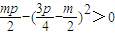 成立,
成立,整理得:
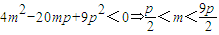 ,且
,且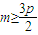 ,
,所以
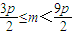 .…(11分)
.…(11分)②若
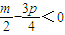 ,即
,即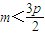 ,只要使
,只要使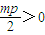 成立,得m>0
成立,得m>0所以
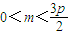 …(13分)
…(13分)由①②得m的取值范围是
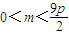 且
且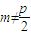 .…(15分)
.…(15分)点评:本题主要考查了抛物线的标准方程、抛物线的简单性质,同时考查了向量的数量积,考查了计算能力.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 如图,已知抛物线C:y2=2px(p>0)的焦点为F,A是抛物线上横坐标为4且位于x轴上方的点. A到抛物线准线的距离等于5,过A作AB垂直于y轴,垂足为B,OB的中点为M(O为坐标原点).
如图,已知抛物线C:y2=2px(p>0)的焦点为F,A是抛物线上横坐标为4且位于x轴上方的点. A到抛物线准线的距离等于5,过A作AB垂直于y轴,垂足为B,OB的中点为M(O为坐标原点). 已知抛物线C:y2=4x,点M(m,0)在x轴的正半轴上,过M的直线l与C相交于A、B两点,O为坐标原点.
已知抛物线C:y2=4x,点M(m,0)在x轴的正半轴上,过M的直线l与C相交于A、B两点,O为坐标原点.