题目内容
坐标空间中,考虑球面S:(x-1)2+(y-2)2+(z-3)2=14与A(1,0,0),B(-1,0,0)两点.请问下列哪些选项是正确的?(1)原点在球面S上 (2)A点在球面S之外部 (3)线段
. | AB |
分析:由于S:(x-1)2+(y-2)2+(z-3)2=14,表示:球心P(1,2,3),半径r=
(1)利用原点O与球心P的距离进行判定;O在球面上.
(2)利用AP的长与半径之间的关系判定A在球面S的内部.
(3)利用AP的长与半径之间的关系判定B在球面S的外部,所以
与球面S相交.
(4)直线AB上距离球心P最近的点即为P在直线AB上的投影点Q.结合向量的去处即可;
(5)利用平面愈接近球心,与球面S所截出的圆面积愈大进行判定.
| 14 |
(1)利用原点O与球心P的距离进行判定;O在球面上.
(2)利用AP的长与半径之间的关系判定A在球面S的内部.
(3)利用AP的长与半径之间的关系判定B在球面S的外部,所以
. |
| AB |
(4)直线AB上距离球心P最近的点即为P在直线AB上的投影点Q.结合向量的去处即可;
(5)利用平面愈接近球心,与球面S所截出的圆面积愈大进行判定.
解答:解:S:(x-1)2+(y-2)2+(z-3)2=14,球心P(1,2,3),半径r=
(1)原点O与球心P的距离
=
=
=r,故O在球面上.
(2)
=
=
<r,故A在球面S的内部.
(3)
=
=
>r,故B在球面S的外部,所以
与球面S相交.
(4)直线AB上距离球心P最近的点即为P在直线AB上的投影点Q.
=(-2,0,0)=-2(1,0,0)
设Q(k,0,0)∵
⊥
,∴(k-1,-2,-3)•(1,0,0)=0?k=1
故Q(1,0,0),即Q=A
(5)平面愈接近球心,与球面S所截出的圆面积愈大.球心P(1,2,3)距离xy平面3个单位,距离yz平面1个单位,
距离xoz平面2个单位;故求面S与yz平面所截出圆面积最大.
故答案为(1)(3)(4).
| 14 |
(1)原点O与球心P的距离
. |
| OP |
| 12+22+32 |
| 14 |
(2)
. |
| AP |
| (1-1)2+(2-0)2+(3-0)2 |
| 13 |
(3)
. |
| BP |
| (-1-1)2+(2-0)2+(3-0)2 |
| 17 |
. |
| AB |
(4)直线AB上距离球心P最近的点即为P在直线AB上的投影点Q.
| AB |
设Q(k,0,0)∵
| PQ |
| AB |
故Q(1,0,0),即Q=A
(5)平面愈接近球心,与球面S所截出的圆面积愈大.球心P(1,2,3)距离xy平面3个单位,距离yz平面1个单位,
距离xoz平面2个单位;故求面S与yz平面所截出圆面积最大.
故答案为(1)(3)(4).
点评:本题主要考查球的空间直角坐标方程与点、球与平面位置关系的判断方法,难易度中.解答的关键是利用到球心的距离与半径的大小关系进行判定.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
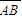 与球面S相交 (4)A点为直线AB上距离球心最近的点 (5)球面S和xy,yz,xz平面分别截出的三个圆中,以与xy平面所截的圆面积为最大.
与球面S相交 (4)A点为直线AB上距离球心最近的点 (5)球面S和xy,yz,xz平面分别截出的三个圆中,以与xy平面所截的圆面积为最大.