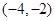题目内容
点P(2,
)是双曲线
-
=1(a>0,b>0)的渐近线上的一点,E,F分别是双曲线的左、右焦点,若
•
=0,则双曲线的方程为( )
| 5 |
| x2 |
| a2 |
| y2 |
| b2 |
| EP |
| FP |
分析:由点在渐近线可得5a2=4b2,由数量积为0可得c2=9,结合a2+b2=c2=9,解之可得答案.
解答:解:由题意可得
=2
,即5a2=4b2,
因为E,F分别是双曲线的左、右焦点,故E(-c,0),F(c,0),
故
•
=(2+c,
)•(2-c,
)=4-c2+5=9-c2=0,即c2=9,
又a2+b2=c2=9,结合5a2=4b2可解得a2=4,b2=5,
故双曲线的方程为
-
=1
故选C

| 5 |
| b |
| a |
因为E,F分别是双曲线的左、右焦点,故E(-c,0),F(c,0),
故
| EP |
| FP |
| 5 |
| 5 |
又a2+b2=c2=9,结合5a2=4b2可解得a2=4,b2=5,
故双曲线的方程为
| x2 |
| 4 |
| y2 |
| 5 |
故选C

点评:本题考查双曲线的标准方程,涉及数量积的运算,属中档题.

练习册系列答案
 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案
相关题目
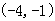 B.
B.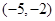 C.
C.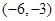 D.
D.