题目内容
已知椭圆 的一个焦点为
的一个焦点为 ,与两坐标轴正半轴分别交于A,B两点(如图),向量
,与两坐标轴正半轴分别交于A,B两点(如图),向量 与向量
与向量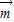 =
= 共线.
共线.(1)求椭圆的方程;
(2)若斜率为k的直线过点C(0,2),且与椭圆交于P,Q两点,求△POC与△QOC面积之比的取值范围.
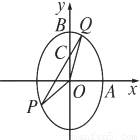
【答案】分析:(1)利用向量共线,确定a,b的关系,结合椭圆的焦点坐标,即可求得椭圆的方程;
(2)直线方程代入椭圆方程,利用韦达定理,即可求得比值的范围.
解答:解:(1)由向量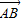 与向量
与向量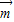 =
=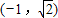 共线,可得
共线,可得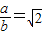
∵焦点为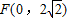 ,∴a2-b2=8,∴b2=8,a2=16
,∴a2-b2=8,∴b2=8,a2=16
∴椭圆的方程为 ;
;
(2)设P(x1,y1),Q(x2,y2),且x1<0,x2>0,
PQ的方程为y=kx+2,代入椭圆方程消去y,可得(2+k2)x2+4kx-12=0
∴x1+x2=-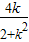 ①,x1x2=-
①,x1x2=-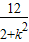 ②
②
设△POC与△QOC面积之比为λ,即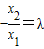
结合①②得(1-λ)x1=- ,λx12=-
,λx12=-
∴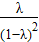 =
=
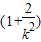 >
>
∴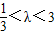
∴△POC与△QOC面积之比的取值范围为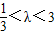 .
.
点评:本题考查椭圆的标准方程,考查直线与椭圆的位置关系,考查向量知识的运用,正确运用韦达定理是关键.
(2)直线方程代入椭圆方程,利用韦达定理,即可求得比值的范围.
解答:解:(1)由向量
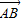 与向量
与向量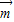 =
=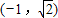 共线,可得
共线,可得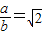
∵焦点为
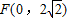 ,∴a2-b2=8,∴b2=8,a2=16
,∴a2-b2=8,∴b2=8,a2=16∴椭圆的方程为
 ;
;(2)设P(x1,y1),Q(x2,y2),且x1<0,x2>0,
PQ的方程为y=kx+2,代入椭圆方程消去y,可得(2+k2)x2+4kx-12=0
∴x1+x2=-
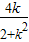 ①,x1x2=-
①,x1x2=-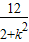 ②
②设△POC与△QOC面积之比为λ,即
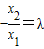
结合①②得(1-λ)x1=-
 ,λx12=-
,λx12=-
∴
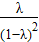 =
=
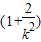 >
>
∴
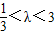
∴△POC与△QOC面积之比的取值范围为
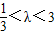 .
.点评:本题考查椭圆的标准方程,考查直线与椭圆的位置关系,考查向量知识的运用,正确运用韦达定理是关键.

练习册系列答案
 每课必练系列答案
每课必练系列答案 巧学巧练系列答案
巧学巧练系列答案
相关题目
已知椭圆的一个焦点为F,若椭圆上存在点P,满足以椭圆短轴为直径的圆与线段PF相切于线段PF的中点,则该椭圆的离心率为( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
 的一个焦点为(0,2)则
的一个焦点为(0,2)则 的值为( )
的值为( )