题目内容
.（本小题满分12分）
已知椭圆的中心在坐标原点
，焦点在
轴上，椭圆的短轴端点和焦点所组成的四边形为正方形，短轴长为2．
（Ⅰ）求椭圆的方程；
（Ⅱ）设直线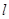
过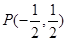
且与椭圆相交于A，B两点，当P是AB的中点时，
求直线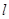的方程．
【答案】
解：设椭圆方程为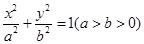
． ……………1分
（Ⅰ）由已知可得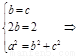
．
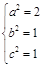……………4分
∴所求椭圆方程为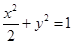
．
……………5分
（Ⅱ）当直线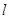
的斜率存在时，
设直线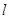的方程为
，
，
，
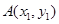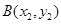………6分
则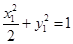
，
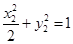，两式相减得：
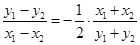． ………8分
∵P是AB的中点，∴
，
，
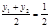代入上式可得直线AB的斜率为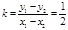
……10分
∴直线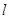的方程为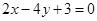
．
当直线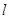的斜率不存在时，将
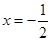代入椭圆方程并解得
，
，
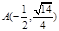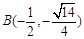这时AB的中点为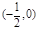
，
∴
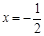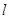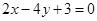不符合题设要求．综上，直线的方程为．…12分
【解析】略
练习册系列答案
特高级教师点拨系列答案
相关题目
，且
。①求
的最大值及最小值；②求
、
、
.现有3名工人独立地从中任选一个项目参与建设.求：
