题目内容
定义在区间[a,b]上的连续函数y=f(x),如果?ξ∈[a,b],使得f(b)-f(a)=f'(ξ)(b-a),则称ξ为区间[a,b]上的“中值点”.下列函数:
①f(x)=3x+2; ②f(x)=x2-x+1; ③f(x)=ln(x+1); ④
在区间[0,1]上“中值点”多于一个的函数序号为________.(写出所有满足条件的函数的序号)
①④
分析:根据题意,“中值点”的几何意义是在区间[0,1]上存在点,使得函数在该点的切线的斜率等于区间[0,1]的两个端点连线的斜率值.分别画出四个函数的图象,如图.由此定义再结合函数的图象与性质,对于四个选项逐个加以判断,即得正确答案.
解答: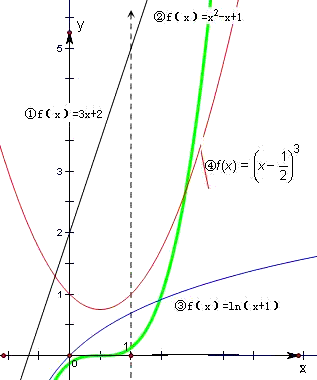 解:根据题意,“中值点”的几何意义是在区间[0,1]上存在点,使得函数在该点的切线的斜率等于区间[0,1]的两个端点连线的斜率值.如图.
解:根据题意,“中值点”的几何意义是在区间[0,1]上存在点,使得函数在该点的切线的斜率等于区间[0,1]的两个端点连线的斜率值.如图.
对于①,根据题意,在区间[0,1]上的任何一点都是“中值点”,故①正确;
对于②,根据“中值点”函数的定义,抛物线在区间[0,1]只存在一个“中值点”,故②不正确;
对于③,f(x)=ln(x+1)在区间[0,1]只存在一个“中值点”,故③不正确;
对于④,根据对称性,函数 在区间[0,1]存在两个“中值点”,故④正确.
在区间[0,1]存在两个“中值点”,故④正确.
故答案为:①④.
点评:本题以命题真假的判断为载体,着重考查了导数及其几何意义等知识点,属于中档题.
分析:根据题意,“中值点”的几何意义是在区间[0,1]上存在点,使得函数在该点的切线的斜率等于区间[0,1]的两个端点连线的斜率值.分别画出四个函数的图象,如图.由此定义再结合函数的图象与性质,对于四个选项逐个加以判断,即得正确答案.
解答:
 解:根据题意,“中值点”的几何意义是在区间[0,1]上存在点,使得函数在该点的切线的斜率等于区间[0,1]的两个端点连线的斜率值.如图.
解:根据题意,“中值点”的几何意义是在区间[0,1]上存在点,使得函数在该点的切线的斜率等于区间[0,1]的两个端点连线的斜率值.如图.对于①,根据题意,在区间[0,1]上的任何一点都是“中值点”,故①正确;
对于②,根据“中值点”函数的定义,抛物线在区间[0,1]只存在一个“中值点”,故②不正确;
对于③,f(x)=ln(x+1)在区间[0,1]只存在一个“中值点”,故③不正确;
对于④,根据对称性,函数
 在区间[0,1]存在两个“中值点”,故④正确.
在区间[0,1]存在两个“中值点”,故④正确.故答案为:①④.
点评:本题以命题真假的判断为载体,着重考查了导数及其几何意义等知识点,属于中档题.

练习册系列答案
相关题目