题目内容
（2012•上海）在平行四边形ABCD中，∠A=
，边AB、AD的长分别为2、1，若M、N分别是边BC、CD上的点，且满足
=
，则
•
的取值范围是
| π |
| 3 |
| ||
|
| ||
|
| AM |
| AN |
[2，5]
[2，5]
．分析：画出图形，建立直角坐标系，利用比例关系，求出M，N的坐标，然后通过二次函数求出数量积的范围．
解答：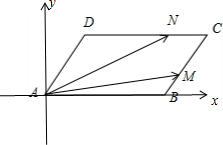
解：建立如图所示的直角坐标系，则B（2，0），A（0，0），
D（
，
），设
=
=λ，λ∈[0，1]，
M（2+
，
），N（
-2λ，
），
所以
•
=（2+
，
）•（
-2λ，
）
=-λ2-2λ+5，因为λ∈[0，1]，二次函数的对称轴为：λ=-1，
所以λ∈[0，1]时，-λ2-2λ+5∈[2，5]．
故答案为：[2，5]．
解：建立如图所示的直角坐标系，则B（2，0），A（0，0），D（
| 1 |
| 2 |
| ||
| 2 |
| ||
|
| ||
|
M（2+
| λ |
| 2 |
| ||
| 2 |
| 5 |
| 2 |
| ||
| 2 |
所以
| AM |
| AN |
| λ |
| 2 |
| ||
| 2 |
| 5 |
| 2 |
| ||
| 2 |
=-λ2-2λ+5，因为λ∈[0，1]，二次函数的对称轴为：λ=-1，
所以λ∈[0，1]时，-λ2-2λ+5∈[2，5]．
故答案为：[2，5]．
点评：本题考查向量的综合应用，平面向量的坐标表示以及数量积的应用，二次函数的最值问题，考查计算能力．
练习册系列答案
阳光试卷单元测试卷系列答案
相关题目