题目内容
 附加题:
附加题:已知f(x)=x-
| 1 | x |
(1)判断函数在区间(-∞,0)上的单调性,并用定义证明;
(2)画出该函数在定义域上的图象.(图象体现出函数性质即可)
分析:(1)设x1<x2<0,则f(x1)-f(x2)=x1-
-x2+
=
,结合已知可判断f(x1)>f(x2),从而可证
(2)f(x)=x-
的定义域为{x|x≠0},为奇函数,f(1)=f(-1)=0,f(x)在区间(-∞,0)上的单调递增,f(x)在区间(0,+∞)上的单调递增,结合函数的性质可画出函数的图象
| 1 |
| x1 |
| 1 |
| x2 |
| (x1-x2)(1+x1x2) |
| x1x2 |
(2)f(x)=x-
| 1 |
| x |
解答: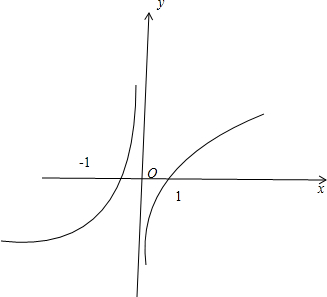 解:(1)函数f(x)在(-∞,0)上递增.…(1分)
解:(1)函数f(x)在(-∞,0)上递增.…(1分)
证明:设x1<x2<0,
则f(x1)-f(x2)=x1-
-x2+
=(x1-x2)+(
-
)
=(x1-x2)+
=
∵x1<x2<0,
∴x1-x2<0,x1x2>0,1+x1x2>0
∴
>0
即f(x1)>f(x2)
∴函数f(x)在区间(-∞,0)上的单调递增…(8分)
(2)∵f(x)=x-
的定义域为{x|x≠0},且为奇函数,f(1)=f(-1)=0
f(x)在区间(-∞,0)上的单调递增,f(x)在区间(0,+∞)上的单调递增…(10分)
图象如图所示
 解:(1)函数f(x)在(-∞,0)上递增.…(1分)
解:(1)函数f(x)在(-∞,0)上递增.…(1分)证明:设x1<x2<0,
则f(x1)-f(x2)=x1-
| 1 |
| x1 |
| 1 |
| x2 |
| 1 |
| x2 |
| 1 |
| x1 |
=(x1-x2)+
| x1-x2 |
| x1x2 |
=
| (x1-x2)(1+x1x2) |
| x1x2 |
∵x1<x2<0,
∴x1-x2<0,x1x2>0,1+x1x2>0
∴
| (x1-x2)(1+x1x2) |
| x1x2 |
即f(x1)>f(x2)
∴函数f(x)在区间(-∞,0)上的单调递增…(8分)
(2)∵f(x)=x-
| 1 |
| x |
f(x)在区间(-∞,0)上的单调递增,f(x)在区间(0,+∞)上的单调递增…(10分)
图象如图所示
点评:本题主要考查了函数的单调性的定义在证明函数的单调性中的应用,画出函数的图象的关键是熟练应用函数的性质

练习册系列答案
 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案
相关题目
 时,求使
时,求使 对任意实数x恒成立的参数a的取值范围.
对任意实数x恒成立的参数a的取值范围. ,
,