题目内容
如图所示,在两个圆盘中,指针在本圆盘每个数所在区域的机会均等,那么两个指针同时落在奇数所在区域的概率是( )


A、
| ||
B、
| ||
C、
| ||
D、
|
分析:首先根据题意,由几何概型的计算公式,计算两个转盘中,指针落在奇数所在区域的概率,进而由相互独立事件概率的乘法公式计算可得答案.
解答:解:根据题意,两个转盘共6个区域,其中有4个是奇数的区域;
由几何概型的计算公式,可得两个转盘中,指针落在奇数所在区域的概率都为
=
;
由独立事件同时发生的概率,得P=
×
=
.
故选A.
由几何概型的计算公式,可得两个转盘中,指针落在奇数所在区域的概率都为
| 4 |
| 6 |
| 2 |
| 3 |
由独立事件同时发生的概率,得P=
| 2 |
| 3 |
| 2 |
| 3 |
| 4 |
| 9 |
故选A.
点评:本题考查概率的计算公式,注意认真审题,认清事件之间的相互关系.

练习册系列答案
相关题目
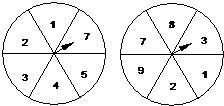 如图所示,在两个圆盘中,指针在本圆盘每个数所在区域的机会均等,那么两个指针同时落在奇数所在区域的概率是
如图所示,在两个圆盘中,指针在本圆盘每个数所在区域的机会均等,那么两个指针同时落在奇数所在区域的概率是 的事件的概率是
的事件的概率是
 B.
B. C.
C. D.
D.
 B.
B.

 D.
D.

 (B).
(B). (C).
(C). (D).
(D).
