题目内容
某纺纱厂生产甲、乙两种棉纱,已知生产甲种棉纱1吨需耗一级子棉2吨、二级子棉1吨;生产乙种棉纱需耗一级子棉1吨、二级子棉2吨,每1吨甲种棉纱的利润是600元,每1吨乙种棉纱的利润是900元,工厂在生产这两种棉纱的计划中要求消耗一级子棉不超过300吨、二级子棉不超过250吨.甲、乙两种棉纱应各生产多少(精确到吨),能使利润总额最大?
生产甲种棉纱117吨,乙种棉纱67吨,能使利润总额达到最大.
解:设生产甲、乙两种棉纱分别为x吨、y吨,利润总额为z元,
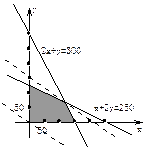
那么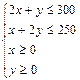 ①
①
z=600x+900y.
作出不等式组①表示的可行域(如右图阴影部分),以及目
标函数对应的直线600x+900y=0,图可看出在点M处z=600x+900y取得最大值,
由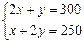 ,得M的坐标为x=
,得M的坐标为x=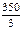 ≈117,y=
≈117,y=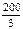 ≈67.
≈67.
答:应生产甲种棉纱117吨,乙种棉纱67吨,能使利润总额达到最大.
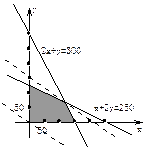
 产品 产品 | 甲种棉纱 (1吨) | 乙种棉纱 (1吨) | 资源限额 (吨) |
| 一级子棉(吨) | 2 | 1 | 300 |
| 二级子棉(吨) | 1 | 2 | 250 |
| 利润(元) | 600 | 900 | |
那么
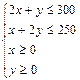 ①
①z=600x+900y.
作出不等式组①表示的可行域(如右图阴影部分),以及目
标函数对应的直线600x+900y=0,图可看出在点M处z=600x+900y取得最大值,
由
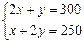 ,得M的坐标为x=
,得M的坐标为x=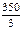 ≈117,y=
≈117,y=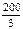 ≈67.
≈67.答:应生产甲种棉纱117吨,乙种棉纱67吨,能使利润总额达到最大.

练习册系列答案
相关题目
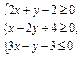 ,试求z=
,试求z=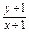 的最大值和最小值.
的最大值和最小值. 产品
产品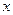 、
、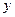 满足约束条件
满足约束条件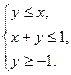
 的最小值,以及相应的
的最小值,以及相应的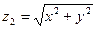 的最大值,以及相应的
的最大值,以及相应的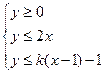 表示一个三角形区域,则实数
表示一个三角形区域,则实数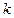 的取值范围是
的取值范围是  ,
, N* ,
N* , N*},
N*}, 
 ,
, ,
, ,若
,若 取最大值时,
取最大值时, ,则实数
,则实数 的取值范围是 ( )
的取值范围是 ( )
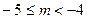

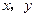 满足
满足 则
则 的最大值是 .
的最大值是 .