题目内容
已知定义域为R的奇函数y=f(x),当x>0时,f(x)=3x-1
(1)求函数f(x)的解析式;
(2)计算f[f(-1)]的值.
(1)求函数f(x)的解析式;
(2)计算f[f(-1)]的值.
分析:(1)只需求得x≤0时的f(x),由奇函数的性质可得f(-0)=-f(0),从而可求得f(0);设x<0,则-x>0,由已知表达式可得f(-x),利用奇函数的性质可得f(-x)与f(x)的关系,可得f(x);
(2)由(1)可求得f(-1),进而可求f[f(-1)];
(2)由(1)可求得f(-1),进而可求f[f(-1)];
解答:解(1)∵f(x)为R上的奇函数,
∴f(-0)=-f(0),即f(0)=-f(0),解得f(0)=0;
设x<0,则-x>0,
∴f(-x)=(
)x-1,则-f(x)=(
)x-1,
得f(x)=-(
)x+1(x<0),
∴f(x)=
;
(2)由(1)知f(-1)=-(
)-1+1=-2,
∴f[f(-1)]=f(-2)=-(
)-2+1=-8.
∴f(-0)=-f(0),即f(0)=-f(0),解得f(0)=0;
设x<0,则-x>0,
∴f(-x)=(
| 1 |
| 3 |
| 1 |
| 3 |
得f(x)=-(
| 1 |
| 3 |
∴f(x)=
|
(2)由(1)知f(-1)=-(
| 1 |
| 3 |
∴f[f(-1)]=f(-2)=-(
| 1 |
| 3 |
点评:本题考查函数的奇偶性的应用,考查函数解析式的求解,属基础题,熟练运用奇偶函数的定义是解决问题的基础.

练习册系列答案
相关题目
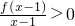 的解集为________(结果用区间表示).
的解集为________(结果用区间表示).