题目内容
已知函数![]() 的反函数为
的反函数为![]() ,定义:若对给定的实数
,定义:若对给定的实数![]() ,函数
,函数![]() 与
与![]() 互为反函数,则称
互为反函数,则称![]() 满足“
满足“![]() 和性质”.
和性质”.
(1)判断函数![]() 是否满足“1和性质”,并说明理由;
是否满足“1和性质”,并说明理由;
(2)若![]() ,其中
,其中![]() 满足“2和性质”,则是否存在实数a,使得
满足“2和性质”,则是否存在实数a,使得
![]() 对任意的
对任意的![]() 恒成立?若存在,求出
恒成立?若存在,求出![]() 的范围;若不存在,请说明理由.
的范围;若不存在,请说明理由.
同下
解析:
(1)函数![]() 的反函数是
的反函数是![]() ,
,![]()
![]() 而
而![]() 其反函数为
其反函数为
![]() , 故函数
, 故函数![]() 不满足“1和性质”;
不满足“1和性质”;
......6分
(2)设函数![]() 满足“2和性质”,
满足“2和性质”,![]()
![]()
![]() ,而
,而![]() ,得反函数
,得反函数![]()
由“2和性质”定义可知![]() =
=![]() 对
对![]() 恒成立,
恒成立,![]()
即函数![]() ,
,![]() ,在
,在![]() 上递减,......9分
上递减,......9分
所以假设存在实数![]() 满足
满足![]()
![]() ,即
,即![]() 对任意的
对任意的![]() 恒成立,它等价于
恒成立,它等价于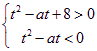 在
在![]() 上恒成立.
上恒成立. ![]() ,
,![]()
![]()
![]() ,易得
,易得![]() .而
.而![]() 知
知![]() 所以
所以![]() .综合以上有当
.综合以上有当![]() 使得
使得![]() 对任意的
对任意的![]() 恒成立.......13分
恒成立.......13分

练习册系列答案
相关题目
 中的数按上小下大,左小右大的原则排列成如图“三角形”所示的数表.设
中的数按上小下大,左小右大的原则排列成如图“三角形”所示的数表.设 是位于这个三角形数表中从上往下数第
是位于这个三角形数表中从上往下数第 行,从左向右数第
行,从左向右数第 个数.
个数. ,求
,求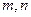 的值;
的值; 的反函数为
的反函数为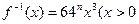 ,
, ),若记三角形数表中从上往下数第
),若记三角形数表中从上往下数第 行各数的和为
行各数的和为 .
. 的前
的前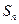 .
.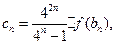 设
设 的前
的前 ,求证:
,求证:

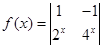 的反函数为
的反函数为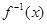 ,则
,则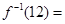 ___________.
___________.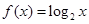 的反函数为
的反函数为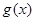 ,且有
,且有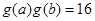 ,若
,若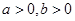 ,则
,则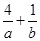 的最小值为( )
的最小值为( )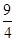 C.4 D.5
C.4 D.5